题目内容
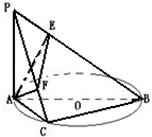
如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,E、F分别是点A在PB、PC上的射影,给出下列结论:①AF⊥PB,②EF⊥PB,③AE⊥BC,④平面AEF⊥平面PBC,⑤△AFE是直角三角形,其中正确的命题的序号是______.

∵AB是⊙O的直径,
∴AC⊥BC,
∵PA⊥⊙O所在平面,
∴PA⊥⊙O所在平面内的所有直线,
∴PA⊥AC,PA⊥AB,PA⊥BC,
∴BC⊥面PAC,
∴BC⊥PC,
∵F是点A在PC上的射影,
∴AF⊥PC,
∵AF∩PC=F,
∴PC⊥面PAC,∴AF⊥BC,
又AF⊥PC,
∴AF⊥面PBC,∴AF⊥PB,∴①正确;
∵AF⊥PB,AF⊥PC,
∴AF⊥面PBC,
∴AF⊥EF,即△AFE是直角三角形,∴⑤正确.
∵AF⊥PB,AE⊥PB,AF∩AE=A,
∴PB⊥面AEF,∴EF⊥PB,∴②正确.
∵AF⊥面PBC,
∴若AE⊥BC,
则AE⊥面PBC,
此时E,F重合,与已知矛盾.∴③错误;
∵AF⊥面PBC,
AF?面AEF,
∴平面AEF⊥平面PBC,
∴④正确.
故答案是:①②④⑤
∴AC⊥BC,
∵PA⊥⊙O所在平面,
∴PA⊥⊙O所在平面内的所有直线,
∴PA⊥AC,PA⊥AB,PA⊥BC,
∴BC⊥面PAC,
∴BC⊥PC,
∵F是点A在PC上的射影,
∴AF⊥PC,
∵AF∩PC=F,
∴PC⊥面PAC,∴AF⊥BC,
又AF⊥PC,
∴AF⊥面PBC,∴AF⊥PB,∴①正确;
∵AF⊥PB,AF⊥PC,
∴AF⊥面PBC,
∴AF⊥EF,即△AFE是直角三角形,∴⑤正确.
∵AF⊥PB,AE⊥PB,AF∩AE=A,
∴PB⊥面AEF,∴EF⊥PB,∴②正确.
∵AF⊥面PBC,
∴若AE⊥BC,
则AE⊥面PBC,
此时E,F重合,与已知矛盾.∴③错误;
∵AF⊥面PBC,
AF?面AEF,
∴平面AEF⊥平面PBC,
∴④正确.
故答案是:①②④⑤

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目