题目内容
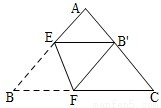
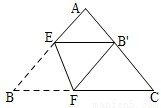
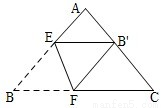
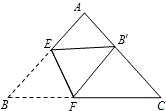 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是 ________.
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是 ________.
 或2
或2分析:由于折叠前后的图形不变,要考虑△B′FC与△ABC相似时的对应情况,分两种情况讨论:①△B′FC∽△ABC时,②△B′CF∽△BCA时,最后利用相似三角形对应边成比例即得BF的长度.
解答:根据△B′FC与△ABC相似时的对应情况,有两种情况:
①△B′FC∽△ABC时,
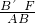 =
=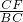 ,
,又因为AB=AC=3,BC=4,B'F=BF,
所以
 =
=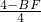 ,
,解得BF=
 ;
;②△B′CF∽△BCA时,
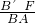 =
=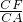 ,
,又因为AB=AC=3,BC=4,B'F=CF,BF=B′F,
所以BF=4-B′F,
解得BF=2.
故BF的长度是
 或2.
或2.故答案为:
 或2.
或2.点评:本题考查对相似三角形性质的理解:(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.

练习册系列答案
相关题目
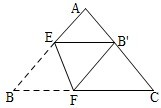 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是