题目内容
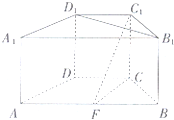 (2010•桂林二模)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=2,BC=CD=1,AA1=1,F在棱AB(不含端点)上,且C1F与底面ABCD所成角的大小为45°
(2010•桂林二模)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=2,BC=CD=1,AA1=1,F在棱AB(不含端点)上,且C1F与底面ABCD所成角的大小为45°(Ⅰ)证明:直线D1B1⊥平面FCC1;
(Ⅱ)求二面角B-FC1-C的大小.
分析:(Ⅰ)构造DM⊥CD,则以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,欲证直线D1B1⊥平面FCC1,只需证明
垂直
,且
垂直
即可;
(Ⅱ)在(Ⅰ)所建立的空间直角坐标系中,平面FCC1的法向量已求得,而平面BFC1的法向量可设出后由其与
、
垂直得到,此时求出两法向量的夹角余弦值,则易得二面角B-FC1-C的余弦值.
| D1B1 |
| CC1 |
| D1B1 |
| C1F |
(Ⅱ)在(Ⅰ)所建立的空间直角坐标系中,平面FCC1的法向量已求得,而平面BFC1的法向量可设出后由其与
| FB |
| FC1 |
解答:证明: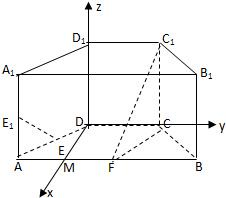 (Ⅰ)因为AB=4,BC=CD=2,F是棱AB的中点,
(Ⅰ)因为AB=4,BC=CD=2,F是棱AB的中点,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则D(0,0,0),D1(0,0,1),B1(
,
,1),
∴
=(
,
,0),
B(
,
,0),C(0,1,0),C1(0,1,1),F(
,
,0),
=(0,0,1),
=(
,-
,0)
∵
•
=0,且
•
=0
故
垂直
,且
垂直
即D1B1⊥CC1且D1B1⊥C1F
又∵CC1∩C1F=C1,
故直线D1B1⊥平面FCC1;
(Ⅱ)由(I)可知平面FCC1的一个法向量
=(
,
,0),
设平面BFC1的法向量为
=(x1,y1,z1),
∵
=(0,1,0),
=(
,-
,0)
则
所以
,
取
=(2,0,
),
则
•
=2×1-
×0+0×
=2,|
|=
=2,
|
|=
=
,
所以 cos<
,
>=
=
=
,
由图可知二面角B-FC1-C为锐角,所以二面角B-FC1-C的余弦值为
.
 (Ⅰ)因为AB=4,BC=CD=2,F是棱AB的中点,
(Ⅰ)因为AB=4,BC=CD=2,F是棱AB的中点,以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则D(0,0,0),D1(0,0,1),B1(
| ||
| 2 |
| 3 |
| 2 |
∴
| D1B1 |
| ||
| 2 |
| 3 |
| 2 |
B(
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| CC1 |
| C1F |
| ||
| 2 |
| 1 |
| 2 |
∵
| D1B1 |
| CC1 |
| D1B1 |
| C1F |
故
| D1B1 |
| CC1 |
| D1B1 |
| C1F |
即D1B1⊥CC1且D1B1⊥C1F
又∵CC1∩C1F=C1,
故直线D1B1⊥平面FCC1;
(Ⅱ)由(I)可知平面FCC1的一个法向量
| n |
| ||
| 2 |
| 3 |
| 2 |
设平面BFC1的法向量为
| n1 |
∵
| FB |
| C1F |
| ||
| 2 |
| 1 |
| 2 |
则
|
|
取
| n1 |
| 3 |
则
| n |
| n1 |
| 3 |
| 3 |
| n |
1+(
|
|
| n1 |
22+0+(
|
| 7 |
所以 cos<
| n |
| n1 |
| ||||
|
|
| 2 | ||
2×
|
| ||
| 7 |
由图可知二面角B-FC1-C为锐角,所以二面角B-FC1-C的余弦值为
| ||
| 7 |
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面垂直的判定,其中建立适当的坐标系,将空间问题转化为向量问题,是解答本题的关键.

练习册系列答案
相关题目