题目内容
已知椭圆C: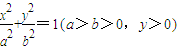 的离心率为
的离心率为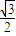 ,A、B为它的左、右焦点,过一定点N(1,0)任作两条互相垂直的直线与C分别交于点P和Q,且|
,A、B为它的左、右焦点,过一定点N(1,0)任作两条互相垂直的直线与C分别交于点P和Q,且|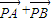 |的最小值为2.
|的最小值为2.(1)求椭圆C的方程;
(2)是否存在直线NP、NQ,使得向量
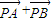 与
与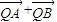 互相垂直?若存在,求出点P、Q的横坐标,若不存在,请说明理由.
互相垂直?若存在,求出点P、Q的横坐标,若不存在,请说明理由.
【答案】分析:(1)设O为坐标原点,易知PO为△PAB的中线,从而可得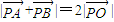 ,易知当点P在短轴上定点时
,易知当点P在短轴上定点时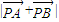 取得最小值2,由此可求得b值,再由离心率及a2=b2+c2可求得a;
取得最小值2,由此可求得b值,再由离心率及a2=b2+c2可求得a;
(2)易知直线NP,NQ斜率均存在,设两直线方程分别为:LNP:y=k(x-1),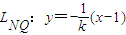 ,由
,由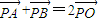 ,
, (O为原点),知只需满足
(O为原点),知只需满足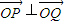 即可,由
即可,由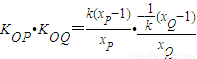 =-1,可得xP+xQ=1①,根据点P、Q在椭圆上得,
=-1,可得xP+xQ=1①,根据点P、Q在椭圆上得,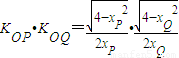 =-1,联立①可得
=-1,联立①可得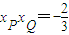 ②,可判断①②构成方程组有解,从而可得结论;
②,可判断①②构成方程组有解,从而可得结论;
解答:解:(1)设O为坐标原点,则PO为△PAB的中线,
∴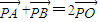 ,
,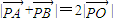 ,
,
因此,当P在短轴上顶点时,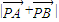 取得最小值2,即2b=2,解得b=1,
取得最小值2,即2b=2,解得b=1,
依题意得: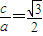 ,即
,即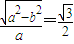 ,即
,即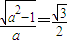 ,∴a2=4,
,∴a2=4,
∴椭圆C的方程为: ;
;
(2)由题意知直线NP,NQ斜率均存在,设为KNP=k, ,
,
则此两直线方程分别为:LNP:y=k(x-1),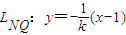 ,
,
又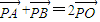 ,
,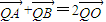 (O为原点),因此,只要满足
(O为原点),因此,只要满足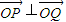 即可,
即可,
故 =-1,化简为:xP+xQ=1,
=-1,化简为:xP+xQ=1,
由半椭圆方程得: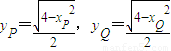 ,则
,则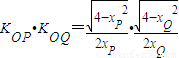 =-1,即
=-1,即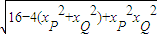 =-4xPxQ,
=-4xPxQ,
令xPxQ=t≤0且xP+xQ=1,故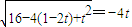 ,
,
化简为:15t2-8t-12=0,解得t=- 或t=
或t=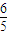 (舍去),∴
(舍去),∴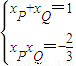 ,
,
解之得: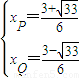 或
或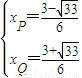 ,
,
因此,直线NP、NQ能使得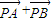 与
与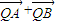 互相垂直.
互相垂直.
点评:本题考查椭圆的标准方程、直线斜率及其方程,考查直线与椭圆的位置关系,考查学生对问题的探究能力及解决问题的能力.
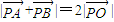 ,易知当点P在短轴上定点时
,易知当点P在短轴上定点时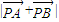 取得最小值2,由此可求得b值,再由离心率及a2=b2+c2可求得a;
取得最小值2,由此可求得b值,再由离心率及a2=b2+c2可求得a;(2)易知直线NP,NQ斜率均存在,设两直线方程分别为:LNP:y=k(x-1),
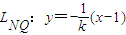 ,由
,由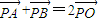 ,
, (O为原点),知只需满足
(O为原点),知只需满足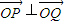 即可,由
即可,由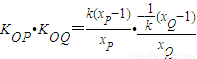 =-1,可得xP+xQ=1①,根据点P、Q在椭圆上得,
=-1,可得xP+xQ=1①,根据点P、Q在椭圆上得,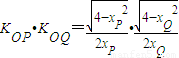 =-1,联立①可得
=-1,联立①可得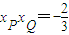 ②,可判断①②构成方程组有解,从而可得结论;
②,可判断①②构成方程组有解,从而可得结论;解答:解:(1)设O为坐标原点,则PO为△PAB的中线,
∴
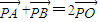 ,
,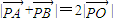 ,
,因此,当P在短轴上顶点时,
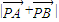 取得最小值2,即2b=2,解得b=1,
取得最小值2,即2b=2,解得b=1,依题意得:
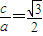 ,即
,即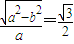 ,即
,即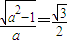 ,∴a2=4,
,∴a2=4,∴椭圆C的方程为:
 ;
;(2)由题意知直线NP,NQ斜率均存在,设为KNP=k,
 ,
,则此两直线方程分别为:LNP:y=k(x-1),
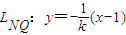 ,
,又
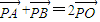 ,
,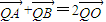 (O为原点),因此,只要满足
(O为原点),因此,只要满足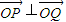 即可,
即可,故
 =-1,化简为:xP+xQ=1,
=-1,化简为:xP+xQ=1,由半椭圆方程得:
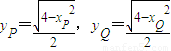 ,则
,则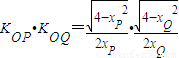 =-1,即
=-1,即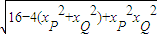 =-4xPxQ,
=-4xPxQ,令xPxQ=t≤0且xP+xQ=1,故
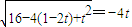 ,
,化简为:15t2-8t-12=0,解得t=-
 或t=
或t=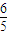 (舍去),∴
(舍去),∴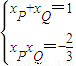 ,
,解之得:
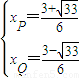 或
或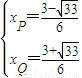 ,
,因此,直线NP、NQ能使得
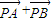 与
与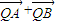 互相垂直.
互相垂直.点评:本题考查椭圆的标准方程、直线斜率及其方程,考查直线与椭圆的位置关系,考查学生对问题的探究能力及解决问题的能力.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、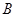 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.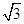
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线