题目内容
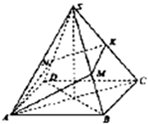 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD的边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心,K是棱SC的中点,过AK作平面与线段SB,SD分别交于M,N(M,N可以是线段的端点).
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD的边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心,K是棱SC的中点,过AK作平面与线段SB,SD分别交于M,N(M,N可以是线段的端点).(1)求直线AK平面SBC所成角的正弦值;
(2)当M是SB中点时,求四棱锥 S-AMKN 的体积.
分析:(1)设AK与平面SBC所成角为θ,由SC=
=
,知CK=
,故cos∠SCA=
=
,由此能够求出直线AK平面SBC所成角的正弦值.
(2)当M是SB的中点时,MK∥BC,由BC∥平面SAD,知MK∥平面SAD,MK∥AN,MK∥AD,故N,D两点重合,由此能求出M是SB中点时,四棱锥 S-AMKN 的体积.
32+(
|
| 11 |
| ||
| 2 |
| ||
|
| ||
| 11 |
(2)当M是SB的中点时,MK∥BC,由BC∥平面SAD,知MK∥平面SAD,MK∥AN,MK∥AD,故N,D两点重合,由此能求出M是SB中点时,四棱锥 S-AMKN 的体积.
解答:解:(1)设AK与平面SBC所成角为θ,
∵SC=
=
,∴CK=
.
∴cos∠SCA=
=
,
∴AK2=AC2+CK2-2AC•CK•cos∠SCA=
.
∴AK=
.
∵VS-ABC=
×
×2×2×3=2=VA-BCS,
∴h=
=
,
∴sinθ=
=
.
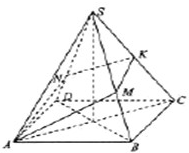
(2)当M是SB的中点时,MK∥BC,
∵BC∥平面SAD,∴MK∥平面SAD,
∴MK∥AN,MK∥AD,
∴N,D两点重合,
∴M到平面SAK的距离为
,
∴S△SAK=
S△SAC=
,
∴M是SB中点时,四棱锥 S-AMKN 的体积:
VS-AMKN=
×S△SAK•
+
×S△SAC•
=
•S△SAK=
×
=
.
∵SC=
32+(
|
| 11 |
| ||
| 2 |
∴cos∠SCA=
| ||
|
| ||
| 11 |
∴AK2=AC2+CK2-2AC•CK•cos∠SCA=
| 27 |
| 4 |
∴AK=
3
| ||
| 2 |
∵VS-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| 6 |
| S△SBC |
3
| ||
| 5 |
∴sinθ=
| h |
| AK |
2
| ||
| 15 |

(2)当M是SB的中点时,MK∥BC,
∵BC∥平面SAD,∴MK∥平面SAD,
∴MK∥AN,MK∥AD,
∴N,D两点重合,
∴M到平面SAK的距离为
| ||
| 2 |
∴S△SAK=
| 1 |
| 2 |
3
| ||
| 2 |
∴M是SB中点时,四棱锥 S-AMKN 的体积:
VS-AMKN=
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
点评:本题考查直线与平面所成角的正弦值的求法,考查四棱锥的体积的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
相关题目
 如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°且
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°且 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.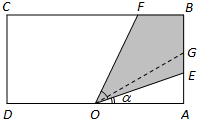 如图一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为
如图一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为