题目内容
已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
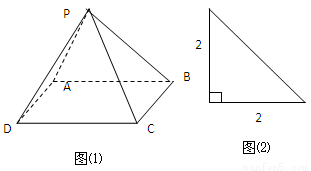
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.
【答案】
⑴利用面面垂直的性质得到线面垂直,然后再由线面垂直证得线线垂直;⑵ ;⑶
;⑶ 。
。
【解析】
试题分析:⑴取AB的中点O,连接PO,因为PA=PB,则PO⊥AB,
又∵ 平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PO 平面PAB,
平面PAB,
∴PO⊥平面ABCD,∴PO⊥AD, 2分
而AD⊥AB,PO∩AB=O,∴AD⊥平面PAB,∴AD⊥PB。 4分
⑵过O作AD的平行线为x轴,以OB、OP所在直线分别为y、z轴,建立如图的空间直角坐标系,则A(0,-1,0),D(2,-1,0),B(0,1,0),C(2,1,0),

 =(2,-1,-2),
=(2,-1,-2), =(0,2,0),cos<
=(0,2,0),cos< ,
, >=
>= =-
=- ,
,
即异面直线PD与AB所成角的余弦值为 。 8分
。 8分
⑶易得平面PAB的一个法向量为n=(1,0 ,0)。
设平面PCD的一个法向量为m=(x,y,z),由⑵知 =(2,-1,-2),
=(2,-1,-2), =(0,-2,0),则
=(0,-2,0),则 ,即
,即 ,解得x=z,
,解得x=z,
令x=1,则m=(1,0,1), .10分
则cos<n,m>= =
= ,
,
即平面PAB与平面PCD所成锐二面角的大小为 。 .12分
。 .12分
考点:本题考查了空间中线面关系
点评:空间各种角问题最终都可以转化为线线角求解,可用空间向量的数量积及其夹角余弦公式求解。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.