题目内容
已知圆的参数方程为
(α为参数),直线l的极坐标方程为3ρcosθ+4ρsinθ+m=0,若圆与直线相切,则实数m=
|
2或-8
2或-8
.分析:把圆的参数方程化为直角坐标方程,把直线l的极坐标方程化为直角坐标方程,利用圆心到直线的距离等于半径求出m 的值.
解答:解:圆的参数方程为
(α为参数),化为普通方程,即(x-1)2+y2=1.
直线3ρcosθ+4ρsinθ+m=0 即 3x+4y+m=0.
已知圆与直线相切,
∴圆心(1,0)到直线的距离等于半径.
∴
=1,解得m=2或m=-8,
故答案为:2或-8.
|
直线3ρcosθ+4ρsinθ+m=0 即 3x+4y+m=0.
已知圆与直线相切,
∴圆心(1,0)到直线的距离等于半径.
∴
| |3+0+m| | ||
|
故答案为:2或-8.
点评:本题考查把参数方程化为普通方程,把极坐标方程化为直角坐标方程的方法,直线和圆相切的性质,把参数方程化为普通方程,把极坐标方程化为直角坐标方程是解题的突破口.

练习册系列答案
相关题目
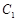 的参数方程为
的参数方程为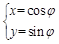 (
(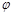 为参数),以坐标原点
为参数),以坐标原点 为极点,x轴的正半轴为极轴建立极坐标系,圆
为极点,x轴的正半轴为极轴建立极坐标系,圆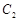 的极坐标方程为
的极坐标方程为 .
.