题目内容
已知函数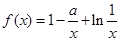 (
(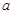 为实常数)。
为实常数)。
(Ⅰ)当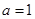 时,求函数
时,求函数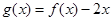 的单调区间;
的单调区间;
(Ⅱ)若函数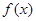 在区间
在区间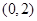 上无极值,求
上无极值,求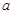 的取值范围;
的取值范围;
(Ⅲ)已知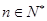 且
且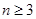 ,求证:
,求证: 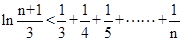 .
.
【答案】
(Ⅰ)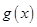 在
在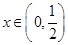 时递增;在
时递增;在 时递减。
时递减。
(Ⅱ)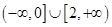 (Ⅲ)见解析
(Ⅲ)见解析
【解析】本试题主要是考查了导数在研究函数极值和单调性方面的运用以及利用导数来证明不等式的综合问题。
(1)因为函数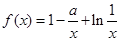 (
( 为实常数)。当
为实常数)。当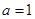 时,求函数
时,求函数 的单调区间,求解导数,然后解不等式得到结论。
的单调区间,求解导数,然后解不等式得到结论。
(2)因为 ,然后对于参数a进行分类讨论得到单调性和极值问题的判定。
,然后对于参数a进行分类讨论得到单调性和极值问题的判定。
(3)由(Ⅱ)知,当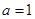 时,
时,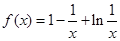 在
在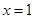 处取得最大值
处取得最大值 .
.
即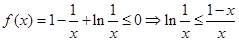 .
.
利用放缩法得打结论。
解:(I)当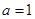 时,
时,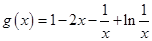 ,其定义域为
,其定义域为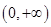 ;
;
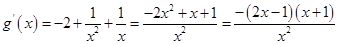 ,
,
令 ,并结合定义域知
,并结合定义域知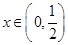 ; 令
; 令 ,并结合定义域知
,并结合定义域知 ;
;
故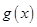 在
在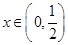 时递增;在
时递增;在 时递减。
时递减。
(II) ,
,
①当 时,
时, ,
, 在
在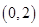 上递减,无极值;
上递减,无极值;
②当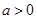 时,
时, 在
在 上递增,在
上递增,在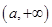 上递减,故
上递减,故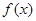 在
在 处取得极大值.要使
处取得极大值.要使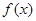 在区间
在区间 上无极值,则
上无极值,则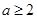 .
.
综上所述, 的取值范围是
的取值范围是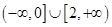 .
.
(Ⅲ)由(Ⅱ)知,当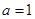 时,
时,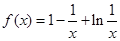 在
在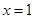 处取得最大值
处取得最大值 .
.
即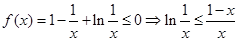 .
.
令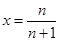 ,则
,则 ,即
,即 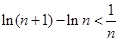 ,
,
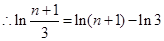


练习册系列答案
相关题目
 已知函数f(x)=x4+ax3+bx2+cx+d(a,b,c,d为实常数)的图象经过三点
已知函数f(x)=x4+ax3+bx2+cx+d(a,b,c,d为实常数)的图象经过三点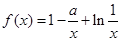 (
(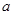 为实常数).
为实常数).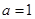 时,求函数
时,求函数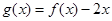 的单调区间;
的单调区间; 在区间
在区间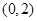 上无极值,求
上无极值,求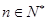 且
且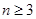 ,求证:
,求证: 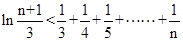 .
.