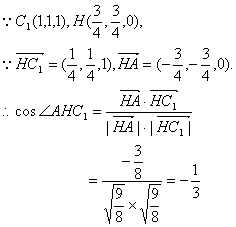题目内容
(04年湖北卷理)(12分)
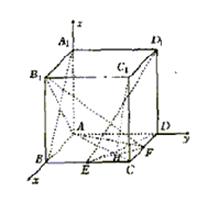
如图,在棱长为1的正方体ABCD―A1B1C1D1中,点E是棱BC的中点,点F是棱
CD上的动点.
(I)试确定点F的位置,使得D1E⊥平面AB1F;
(II)当D1E⊥平面AB1F时,求二面角C1―EF―A的大小(结果用反三角函数值表示).

解析:解法一:(I)连结A1B,则A1B是D1E在面ABB1A;内的射影
∵AB1⊥A1B,∴D1E⊥AB1,
于是D1E⊥平面AB1F![]() D1E⊥AF.
D1E⊥AF.
连结DE,则DE是D1E在底面ABCD内的射影.
∴D1E⊥AF![]() DE⊥AF.
DE⊥AF.
∵ABCD是正方形,E是BC的中点.
∴当且仅当F是CD的中点时,DE⊥AF,
即当点F是CD的中点时,D1E⊥平面AB1F.…………6分
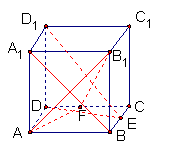
(II)当D1E⊥平面AB1F时,由(I)知点F是CD的中点.
又已知点E是BC的中点,连结EF,则EF∥BD. 连结AC,
设AC与EF交于点H,则CH⊥EF,连结C1H,则CH是
C1H在底面ABCD内的射影.
C1H⊥EF,即∠C1HC是二面角C1―EF―C的平面角.
在Rt△C1CH中,∵C1C=1,CH=![]() AC=
AC=![]() ,
,
∴tan∠C1HC=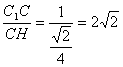 .
.
∴∠C1HC=arctan![]() ,从而∠AHC1=
,从而∠AHC1=![]() .
.
故二面角C1―EF―A的大小为![]() .
.
解法二:以A为坐标原点,建立如图所示的空间直角坐标系
|
(1)设DF=x,则A(0,0,0),B(1,0,0),D(0,1,0),
A1(0,0,1),B(1,0,1),D1(0,1,1),E![]() ,F(x,1,0)
,F(x,1,0)

(1)当D1E⊥平面AB1F时,F是CD的中点,又E是BC的中点,连结EF,则EF∥BD. 连结AC,设AC与EF交于点H,则AH⊥EF. 连结C1H,则CH是C1H在底面ABCD内的射影.
∴C1H⊥EF,即∠AHC1是二面角C1―EF―A的平面角.