题目内容
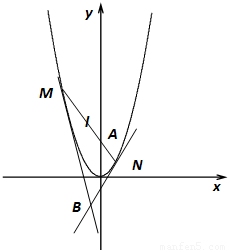
如图,已知过点A(0,1)的直线l与抛物线C:y=x2交于M,N两点,又抛物线C在M,N两点处的两切线交于点B,M,N两点的横坐标分别为x1,x2.(1)求x1x2的值;
(2)求B点的纵坐标t的值.
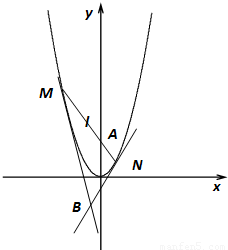
【答案】分析:(1)设直线l的方程为y=kx+1,代入y=x2,利用韦达定理可求x1x2的值;
(2)确定切线方程,求得交点坐标,利用(1)的结论,即可求B点的纵坐标t的值.
解答:解:(1)设直线l的方程为y=kx+1,代入y=x2,可得x2-kx-1=0
∵M,N两点的横坐标分别为x1,x2,
∴x1x2=-1;
(2)由y=x2,得y′=2x,
∴抛物线y=x2在点M(x1,y1)、N(x2,y2)处的切线的斜率分别为2x1,2x2,
∴抛物线C在M,N两点处的两切线方程分别为y-y1=2x1(x-x1),y-y2=2x2(x-x2),
即为y=2x1x-x12,y=2x2x-x22,
∴x2y=2x1x2x-x2x12,x1y=2x1x2x-x1x22,
∵x1x2=-1
∴两式相减,可得B点的纵坐标t=-1.
点评:本题考查直线与抛物线的位置关系,考查抛物线的切线方程,考查学生的计算能力,属于中档题.
(2)确定切线方程,求得交点坐标,利用(1)的结论,即可求B点的纵坐标t的值.
解答:解:(1)设直线l的方程为y=kx+1,代入y=x2,可得x2-kx-1=0
∵M,N两点的横坐标分别为x1,x2,
∴x1x2=-1;
(2)由y=x2,得y′=2x,
∴抛物线y=x2在点M(x1,y1)、N(x2,y2)处的切线的斜率分别为2x1,2x2,
∴抛物线C在M,N两点处的两切线方程分别为y-y1=2x1(x-x1),y-y2=2x2(x-x2),
即为y=2x1x-x12,y=2x2x-x22,
∴x2y=2x1x2x-x2x12,x1y=2x1x2x-x1x22,
∵x1x2=-1
∴两式相减,可得B点的纵坐标t=-1.
点评:本题考查直线与抛物线的位置关系,考查抛物线的切线方程,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知过点A(0,1)的直线l与抛物线C:y=x2交于M,N两点,又抛物线C在M,N两点处的两切线交于点B,M,N两点的横坐标分别为x1,x2.
如图,已知过点A(0,1)的直线l与抛物线C:y=x2交于M,N两点,又抛物线C在M,N两点处的两切线交于点B,M,N两点的横坐标分别为x1,x2.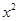 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.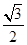 的椭圆
的椭圆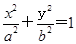 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
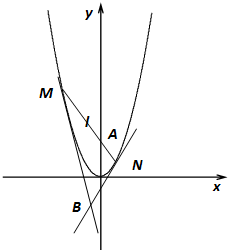 如图,已知过点A(0,1)的直线l与抛物线C:y=x2交于M,N两点,又抛物线C在M,N两点处的两切线交于点B,M,N两点的横坐标分别为x1,x2.
如图,已知过点A(0,1)的直线l与抛物线C:y=x2交于M,N两点,又抛物线C在M,N两点处的两切线交于点B,M,N两点的横坐标分别为x1,x2.