题目内容
已知函数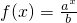 的图象过点
的图象过点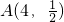 和B(5,1).
和B(5,1).
①求函数f(x)的解析式;②函数f(x)的反函数;③设an=log2f(n),n是正整数,是数列的前项和Sn,解关于的不等式an≤Sn.
解:(1)∵函数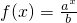 的图象过点
的图象过点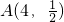 和B(5,1),
和B(5,1),
∴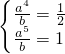 ,解得a=2,b=32,
,解得a=2,b=32,
∴f(x)=2x-5.
(2)设y=f(x)=2x-5,
则x-5=log2y,
x=log2y+5,
x,y互换,得f-1(x)=5+log2x(x>0);
(3)∵an=log2f(n)=log2(2n-5)=n-5,
∴{an}是首项为-4,公差为1的等差数列,
∴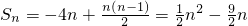 ,
,
∵an≤Sn,
∴n-5≤ ,
,
解得:{n∈N+|n=1或n≥10}.
故答案为:{n∈N+|n=1或n≥10}.
分析:(1)函数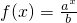 的图象过点
的图象过点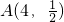 和B(5,1),知
和B(5,1),知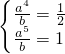 ,由此能求出f(x).
,由此能求出f(x).
(2)设y=f(x)=2x-5,则x-5=log2y,x=log2y+5,x,y互换,得f-1(x)=5+log2x(x>0).
(3)由an=log2f(n)=log2(2n-5)=n-5,知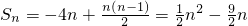 ,由an≤Sn,解不等式n-5≤
,由an≤Sn,解不等式n-5≤ ,能得到{n∈N+|n=1或n≥10}.
,能得到{n∈N+|n=1或n≥10}.
点评:本题考查函数解析式的求法和数列与不等式的综合,解题时要认真审题,注意反函数的灵活运用.
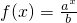 的图象过点
的图象过点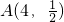 和B(5,1),
和B(5,1),∴
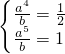 ,解得a=2,b=32,
,解得a=2,b=32,∴f(x)=2x-5.
(2)设y=f(x)=2x-5,
则x-5=log2y,
x=log2y+5,
x,y互换,得f-1(x)=5+log2x(x>0);
(3)∵an=log2f(n)=log2(2n-5)=n-5,
∴{an}是首项为-4,公差为1的等差数列,
∴
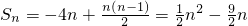 ,
,∵an≤Sn,
∴n-5≤
 ,
,解得:{n∈N+|n=1或n≥10}.
故答案为:{n∈N+|n=1或n≥10}.
分析:(1)函数
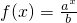 的图象过点
的图象过点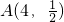 和B(5,1),知
和B(5,1),知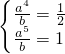 ,由此能求出f(x).
,由此能求出f(x).(2)设y=f(x)=2x-5,则x-5=log2y,x=log2y+5,x,y互换,得f-1(x)=5+log2x(x>0).
(3)由an=log2f(n)=log2(2n-5)=n-5,知
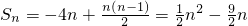 ,由an≤Sn,解不等式n-5≤
,由an≤Sn,解不等式n-5≤ ,能得到{n∈N+|n=1或n≥10}.
,能得到{n∈N+|n=1或n≥10}.点评:本题考查函数解析式的求法和数列与不等式的综合,解题时要认真审题,注意反函数的灵活运用.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
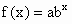 的图象过点
的图象过点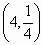 和B(5,1).
和B(5,1).
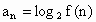 ,n是正整数,
,n是正整数,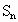 是数列
是数列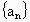 的前n项和,解关于n的不等式
的前n项和,解关于n的不等式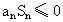 ;
;
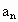 与
与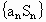 中的项?若是,则求出相应的项数;若不是则说明理由.
中的项?若是,则求出相应的项数;若不是则说明理由.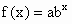 的图象过点
的图象过点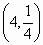 和B(5,1).
和B(5,1).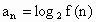 ,n是正整数,
,n是正整数,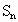 是数列
是数列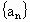 的前n项和,解关于n的不等式
的前n项和,解关于n的不等式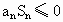 ;
;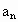 与
与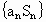 中的项?若是,则求出相应的项数;若不是则说明理由.
中的项?若是,则求出相应的项数;若不是则说明理由.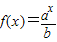 的图象过点
的图象过点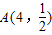 和B(5,1).
和B(5,1).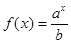 的图象过点
的图象过点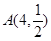 和
和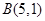 .
.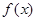 的解析式;
的解析式;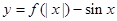 的零点的个数(不必计算说明);
的零点的个数(不必计算说明);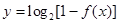 在其定义域上的单调性。
在其定义域上的单调性。