题目内容
已知
，则函数f（x）=
的最小正周期为________．
1
分析：利用两个向量数量积公式可得函数f（x）=sinπx•（2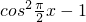
）+cos2πx，再利用三角函数的恒等变换化简为
+
sin（2πx+
），由此求得函数的最小正周期．
解答：函数f（x）==sinπx•（2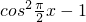）+cos2πx=sinπx•cosπx+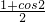
=+（sin2πx+cos2πx）=+sin（2πx+），
故函数的最小正周期为 T=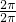
=π1，
故答案为 1．
点评：本题主要考查两个向量数量积公式的应用，三角函数的恒等变换及化简求值，三角函数的周期性以及求法，属于中档题．
分析：利用两个向量数量积公式可得函数f（x）=sinπx•（2
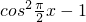）+cos2πx，再利用三角函数的恒等变换化简为+sin（2πx+），由此求得函数的最小正周期．解答：函数f（x）=
=sinπx•（2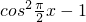）+cos2πx=sinπx•cosπx+=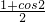
+（sin2πx+cos2πx）=+sin（2πx+），故函数的最小正周期为 T=
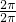=π1，故答案为 1．
点评：本题主要考查两个向量数量积公式的应用，三角函数的恒等变换及化简求值，三角函数的周期性以及求法，属于中档题．
练习册系列答案
相关题目
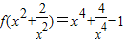，则函数f（x）的最小值是（ ）
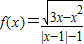，则函数f（x）的定义域为 ．
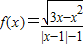，则函数f（x）的定义域为（ ）
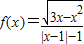，则函数f（x）的定义域为（ ）
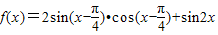，则函数f（x）得最小正周期是 ．