题目内容
已知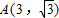 ,O是原点,点P(x,y)的坐标满足
,O是原点,点P(x,y)的坐标满足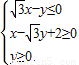 ,
,(1)求
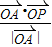 的最大值.;(2)求
的最大值.;(2)求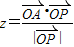 的取值范围.
的取值范围.
【答案】分析:(1)做出满足条件足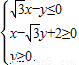 的可行域,根据平面向量数量积的几何意义,可得目标函数
的可行域,根据平面向量数量积的几何意义,可得目标函数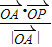 表示
表示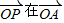 上的投影,过P作
上的投影,过P作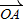 的垂线PH,垂足为H,易得当P在可行域内移动到直线
的垂线PH,垂足为H,易得当P在可行域内移动到直线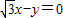 和直线
和直线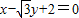 的交点时,目标函数有最大值.
的交点时,目标函数有最大值.
(2)结合(1)的结论,可得当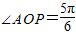 时,目标函数有最小值,当
时,目标函数有最小值,当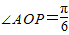 时,目标函数有最大值,进而得到
时,目标函数有最大值,进而得到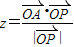 的取值范围.
的取值范围.
解答:解: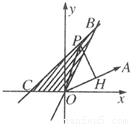 (1)作出可行域如图,则
(1)作出可行域如图,则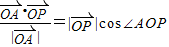 ,
,
又∠AOP是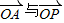 的夹角,
的夹角,
∴目标函数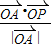 表示
表示 上的投影,
上的投影,
过P作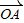 的垂线PH,垂足为H,
的垂线PH,垂足为H,
当P在可行域内移动到直线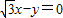 和直线
和直线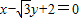 的交点
的交点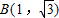 时,
时,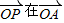 上的投影为
上的投影为 最大,此时
最大,此时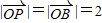 ,∠AOP=∠AOB=
,∠AOP=∠AOB=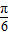 ,
,
∴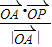 的最大值为
的最大值为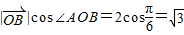
(2)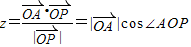 =
=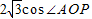 ,
,
因为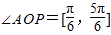 ,所以当
,所以当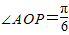 时,
时,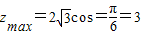 ;
;
当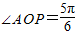 时,
时,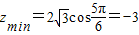 .∴
.∴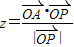 的取值范围为[-3,3].
的取值范围为[-3,3].
点评:本题考查的知识点是简单线性规划的应用,平面向量数量积的运算,余弦函数的性质,其中根据平面向量数量积运算的几何意义,分析出目标函数的几何意义,是解答本题的关键.
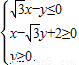 的可行域,根据平面向量数量积的几何意义,可得目标函数
的可行域,根据平面向量数量积的几何意义,可得目标函数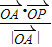 表示
表示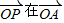 上的投影,过P作
上的投影,过P作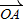 的垂线PH,垂足为H,易得当P在可行域内移动到直线
的垂线PH,垂足为H,易得当P在可行域内移动到直线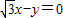 和直线
和直线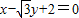 的交点时,目标函数有最大值.
的交点时,目标函数有最大值.(2)结合(1)的结论,可得当
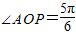 时,目标函数有最小值,当
时,目标函数有最小值,当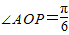 时,目标函数有最大值,进而得到
时,目标函数有最大值,进而得到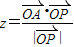 的取值范围.
的取值范围.解答:解:
 (1)作出可行域如图,则
(1)作出可行域如图,则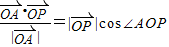 ,
,又∠AOP是
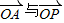 的夹角,
的夹角,∴目标函数
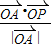 表示
表示 上的投影,
上的投影,过P作
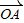 的垂线PH,垂足为H,
的垂线PH,垂足为H,当P在可行域内移动到直线
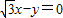 和直线
和直线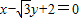 的交点
的交点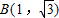 时,
时,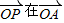 上的投影为
上的投影为 最大,此时
最大,此时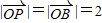 ,∠AOP=∠AOB=
,∠AOP=∠AOB=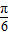 ,
,∴
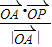 的最大值为
的最大值为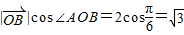
(2)
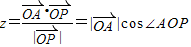 =
=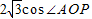 ,
,因为
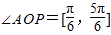 ,所以当
,所以当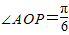 时,
时,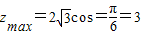 ;
;当
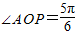 时,
时,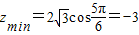 .∴
.∴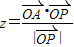 的取值范围为[-3,3].
的取值范围为[-3,3].点评:本题考查的知识点是简单线性规划的应用,平面向量数量积的运算,余弦函数的性质,其中根据平面向量数量积运算的几何意义,分析出目标函数的几何意义,是解答本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
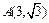 ,O是原点,点P(x, y)的坐标满足
,O是原点,点P(x, y)的坐标满足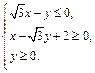

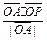 的最大值.;(2)求
的最大值.;(2)求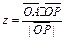 的取值范围.
的取值范围.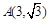 ,O是原点,点P(x, y)的坐标满足
,O是原点,点P(x, y)的坐标满足
 的最大值.;(2)求
的最大值.;(2)求 的取值范围.
的取值范围.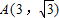 ,O是原点,点P(x,y)的坐标满足
,O是原点,点P(x,y)的坐标满足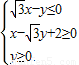 ,
, 的最大值.;(2)求
的最大值.;(2)求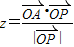 的取值范围.
的取值范围.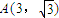 ,O为原点,点P(x,y)的坐标满足
,O为原点,点P(x,y)的坐标满足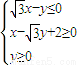 ,则
,则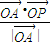 的最大值是 ,此时点P的坐标是 .
的最大值是 ,此时点P的坐标是 .