△ABC为正三角形.P是△ABC所在平面外一点.且PA=PB=PC.△APB与△ABC的面积之比为2:3.则二面角P-AB-C的大小为( ) A.90°B.45°C.60°D.30° 题目和参考答案——青夏教育精英家教网—

题目内容

△ABC为正三角形，P是△ABC所在平面外一点，且PA=PB=PC，△APB与△ABC的面积之比为2：3，则二面角P-AB-C的大小为（　　）

A、90°

B、45°

C、60°

D、30°

分析：取AB的中点D，连接PD，CD，由垂线定理可得∠PDC即为二面角P-AB-C的平面角，根据已知中，△APB与△ABC的面积之比为2：3，解三角形PDC，即可求出答案．

解答：解：取AB的中点D，连接PD，CD，
由△ABC为正三角形可得CD⊥AB
由PA=PB可得PD⊥AB
则∠PDC即为二面角P-AB-C的平面角
设△ABC的边长为2，则参CD=

∵△APB与△ABC的面积之比为2：3
∴PD=

，则PC=

则cos∠PDC=

PD2+CD2-PC2

2•PD•CD

∴∠PDC=60°
故选C

点评：本题考查的知识点是二面角的平面角的求法，其中根据三垂线定理确定二面角的平面角是解答本题的关键．

练习册系列答案

相关题目

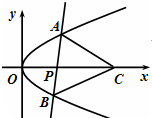设直线l与抛物线y²=2px（p＞0）交于A，B两点，已知当直线l经过抛物线的焦点且与x轴垂直时，△OAB的面积为

（O为坐标原点）．
（1）求抛物线的方程；
（2）当直线l经过点P（a，0）（a＞0）且与x轴不垂直时，若在x轴上存在点C，使得△ABC为正三角形，求a的取值范围．

在△ABC中，角A，B，C所对应的边分别为a，b，c，若实数λ，μ满足a+b=λc，ab=μc²，则称数对（λ，μ）为△ABC的“Hold对”，现给出下列四个命题：
①若△ABC的“Hold对”为（2，1），则△ABC为正三角形；
②若△ABC的“Hold对”为(2，

)，则△ABC为锐角三角形；
③若△ABC的“Hold对”为(

，

)，则△ABC为钝角三角形；
④若△ABC是以C为直角顶点的直角三角形，则以“Hold对”（λ，μ）为坐标的点构成的图形是矩形，其面积为

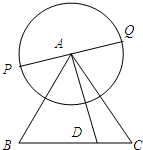如图△ABC为正三角形，边长为2，以点A为圆心，1为半径作圆，PQ为圆A的任意一条直径．
（1）若

的值是否会随点P的变化而变化，请说明理由．

△ABC的内角A、B、C的对边分别为a、b、c，三边长a，b、c成等比数列．
（1）若B=

，求证：△ABC为正三角形；
（2）若B=

，求sin(2A-

)的值．

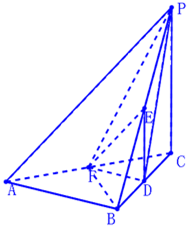如图，在三棱锥P-ABC中，PC⊥平面ABC，△ABC为正三角形，D、E、F分别是BC，PB，CA的中点．
（1）证明平面PBF⊥平面PAC；
（2）判断AE是否平行于平面PFD，并说明理由；
（3）若PC=AB=2，求三棱锥P-DEF的体积．

试题分类