题目内容
如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2。 E、F分别是线段AB、BC上的点,且EB= FB=1.
(1) 求二面角C—DE—C1的余弦值;
(2) 求直线EC1与FD1所成的余弦值.

【答案】
解:(I)(法一)矩形ABCD中过C作CH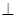 DE于H,连结C1H
DE于H,连结C1H
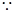 CC1
CC1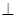 面ABCD,CH为C1H在面ABCD上的射影
面ABCD,CH为C1H在面ABCD上的射影
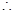 C1H
C1H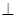 DE
DE
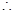
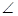 C1HC为二面角C—DE—C1的平面角
C1HC为二面角C—DE—C1的平面角
矩形ABCD中得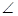 EDC=
EDC=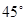 ,
,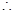
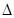 DCH中得CH=
DCH中得CH=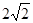 ,
,
又CC1=2,
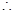
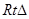 C1HC中,
C1HC中,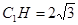 ,
,
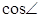 C1HC
C1HC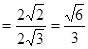
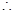 二面角C—DE—C1的余弦值为
二面角C—DE—C1的余弦值为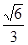 7分
7分
(2)以D为原点,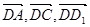 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
设EC1与FD1所成角为β,则
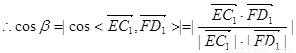
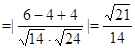
故EC1与FD1所成角的余弦值为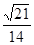 14分
14分
(法二)(1)以D为原点,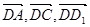 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
于是, ,
,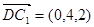 ,
,
设向量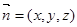 与平面C1DE垂直,则有
与平面C1DE垂直,则有
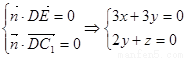 ,
,
令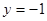 ,则
,则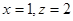
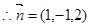
又面CDE的法向量为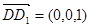
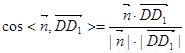
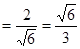 7分
7分
由图,二面角C—DE—C1为锐角,故二面角C—DE—C1的余弦值为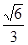 8分
8分
(II)设EC1与FD1所成角为β,则
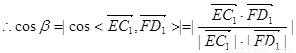
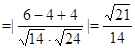
故EC1与FD1所成角的余弦值为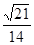 14分
14分
【解析】略

练习册系列答案
相关题目


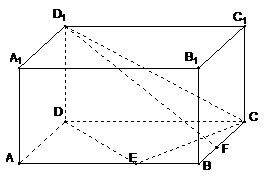 如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2。 E、F分别是线段AB、BC上的点,且EB= FB=1.
如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2。 E、F分别是线段AB、BC上的点,且EB= FB=1.