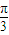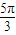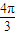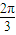题目内容
使函数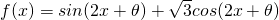 的图象关于原点对称,且满足对于
的图象关于原点对称,且满足对于 内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是
内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是
- A.

- B.

- C.

- D.

D
分析:函数f(x)图象关于原点对称,满足f(0)=0,算出tanθ=- ,得θ=
,得θ= +kπ(k∈Z).再根据函数f(x)区间
+kπ(k∈Z).再根据函数f(x)区间 内恒有(x1-x2)[f(x1)-f(x2)]<0,得函数f(x)为减函数,利用辅助角公式并结合函数y=Asin(ωx+φ)的性质讨论f(x)的单调减区间,即可得到取k=0,得θ=
内恒有(x1-x2)[f(x1)-f(x2)]<0,得函数f(x)为减函数,利用辅助角公式并结合函数y=Asin(ωx+φ)的性质讨论f(x)的单调减区间,即可得到取k=0,得θ= 时满足题设的两个条件.
时满足题设的两个条件.
解答:∵函数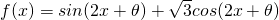 的图象关于原点对称,
的图象关于原点对称,
∴函数f(x)是奇函数,满足f(0)=sinθ+ cosθ=0,
cosθ=0,
得tanθ=- ,θ=
,θ= +kπ,k∈Z
+kπ,k∈Z
∵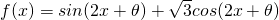 =2sin(2x+θ+
=2sin(2x+θ+ )
)
满足在区间 内恒有(x1-x2)[f(x1)-f(x2)]<0,即函数为减函数
内恒有(x1-x2)[f(x1)-f(x2)]<0,即函数为减函数
∴θ+ ≤2x+θ+
≤2x+θ+ ≤θ+
≤θ+ ,
,
令t=2x+θ+ ,得集合M={t|θ+
,得集合M={t|θ+ ≤t≤θ+
≤t≤θ+ },且M?[
},且M?[ +2mπ,
+2mπ, +2mπ],m∈Z.
+2mπ],m∈Z.
由此可得:取k=m=0,得θ= ,M=[π,
,M=[π, }满足题设的两个条件
}满足题设的两个条件
故选:D
点评:本题给出三角函数的图象关于原点对称,并且在已知一个单调减区间的情况下求参数的值,着重考查了三角函数的图象与性质、三角恒等变形和函数的单调性等知识,属于中档题.
分析:函数f(x)图象关于原点对称,满足f(0)=0,算出tanθ=-
 ,得θ=
,得θ= +kπ(k∈Z).再根据函数f(x)区间
+kπ(k∈Z).再根据函数f(x)区间 内恒有(x1-x2)[f(x1)-f(x2)]<0,得函数f(x)为减函数,利用辅助角公式并结合函数y=Asin(ωx+φ)的性质讨论f(x)的单调减区间,即可得到取k=0,得θ=
内恒有(x1-x2)[f(x1)-f(x2)]<0,得函数f(x)为减函数,利用辅助角公式并结合函数y=Asin(ωx+φ)的性质讨论f(x)的单调减区间,即可得到取k=0,得θ= 时满足题设的两个条件.
时满足题设的两个条件.解答:∵函数
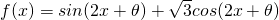 的图象关于原点对称,
的图象关于原点对称,∴函数f(x)是奇函数,满足f(0)=sinθ+
 cosθ=0,
cosθ=0,得tanθ=-
 ,θ=
,θ= +kπ,k∈Z
+kπ,k∈Z∵
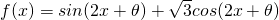 =2sin(2x+θ+
=2sin(2x+θ+ )
)满足在区间
 内恒有(x1-x2)[f(x1)-f(x2)]<0,即函数为减函数
内恒有(x1-x2)[f(x1)-f(x2)]<0,即函数为减函数∴θ+
 ≤2x+θ+
≤2x+θ+ ≤θ+
≤θ+ ,
,令t=2x+θ+
 ,得集合M={t|θ+
,得集合M={t|θ+ ≤t≤θ+
≤t≤θ+ },且M?[
},且M?[ +2mπ,
+2mπ, +2mπ],m∈Z.
+2mπ],m∈Z.由此可得:取k=m=0,得θ=
 ,M=[π,
,M=[π, }满足题设的两个条件
}满足题设的两个条件故选:D
点评:本题给出三角函数的图象关于原点对称,并且在已知一个单调减区间的情况下求参数的值,着重考查了三角函数的图象与性质、三角恒等变形和函数的单调性等知识,属于中档题.

练习册系列答案
相关题目
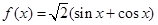 , 给出下列四个命题:
, 给出下列四个命题: 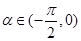 , 使
, 使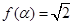 ;
;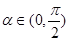 , 使
, 使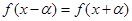 恒成立;
恒成立; 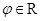 , 使函数
, 使函数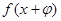 的图象关于坐标原点成中心对称;
的图象关于坐标原点成中心对称; 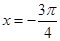 对称;
对称;
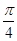 就能得到
就能得到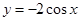 的图象
的图象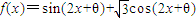 的图象关于原点对称,且满足对于
的图象关于原点对称,且满足对于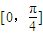 内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是( )
内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是( )