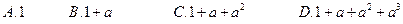题目内容
用数学归纳法证明“当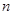 为正奇数时,
为正奇数时,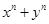 能被
能被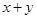 整除”,第二步归纳假
整除”,第二步归纳假
设应该写成( )
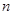 为正奇数时,
为正奇数时,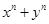 能被
能被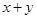 整除”,第二步归纳假
整除”,第二步归纳假设应该写成( )
A.假设当 时, 时, 能被 能被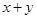 整除 整除 |
B.假设当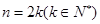 时, 时, 能被 能被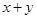 整除 整除 |
C.假设当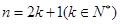 时, 时, 能被 能被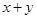 整除 整除 |
D.假设当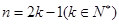 时, 时,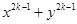 能被 能被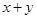 整除 整除 |
D
注意n为正奇数,观察第一步取到1,即可推出第二步的假设.
解:根据数学归纳法的证明步骤,注意n为奇数,所以第二步归纳假设应写成:假设n=2k-1(k∈N*)正确,再推n=2k+1正确;故选D.
本题是基础题,不仅注意第二步的假设,还要使n=2k-1能取到1,是解好本题的关键.
解:根据数学归纳法的证明步骤,注意n为奇数,所以第二步归纳假设应写成:假设n=2k-1(k∈N*)正确,再推n=2k+1正确;故选D.
本题是基础题,不仅注意第二步的假设,还要使n=2k-1能取到1,是解好本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的各项均为正数,
的各项均为正数,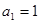 ,
,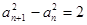
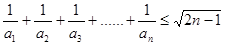 对一切
对一切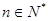 恒成立。
恒成立。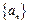 的前
的前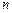 项和
项和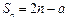 ,先计算数列的前4项,后猜想
,先计算数列的前4项,后猜想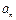 并证明之.
并证明之.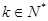 )时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立( ).
)时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立( ).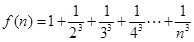 ,
,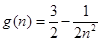 ,
,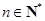 .
. 时,试比较
时,试比较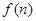 与
与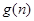 的大小关系;
的大小关系;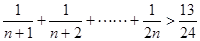 时,由k到k+1,不等式左端的变化是( )
时,由k到k+1,不等式左端的变化是( ) 项
项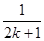 和
和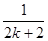 两项
两项 一项
一项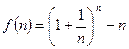 ,其中
,其中 为正整数.
为正整数. ,
, ,
,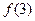 的值;
的值; 的正整数
的正整数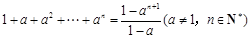 ”时,验证当
”时,验证当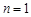 时,等式的左边为 .
时,等式的左边为 .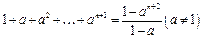 ,在验证
,在验证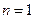 成立时,左边计算所得的项是
成立时,左边计算所得的项是