题目内容
已知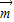 =(1,1),向量
=(1,1),向量 与
与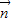 的夹角为
的夹角为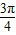 ,且
,且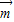 •
• =-1.
=-1.(1)求向量
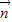 ;
;(2)若
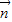 与
与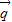 =(1,0)的夹角为
=(1,0)的夹角为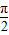 ,
,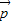 =(cosA,2cos2
=(cosA,2cos2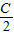 )其中A、C为△ABC的内角,且A+C=
)其中A、C为△ABC的内角,且A+C=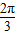 ,求|
,求|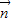 +
+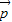 |的最小值.
|的最小值.
【答案】分析:(1)设出向量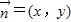 ,根据数量积的定义及坐标运算分别得出两个方程,解出即可;
,根据数量积的定义及坐标运算分别得出两个方程,解出即可;
(2)根据向量的运算及三角运算得出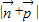 关于角A的三角表达式,再利用三角函数的单调性即可求出其最小值.
关于角A的三角表达式,再利用三角函数的单调性即可求出其最小值.
解答:解:(1)设向量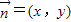 ,∵
,∵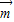 =(1,1),向量
=(1,1),向量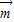 与
与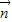 的夹角为
的夹角为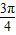 ,且
,且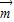 •
•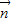 =-1.
=-1.
∴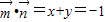 ,
,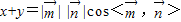 =
=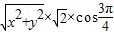 =-
=-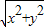 ,
,
即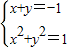 ,解得
,解得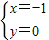 或
或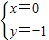 ,
,
∴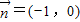 或(0,-1).
或(0,-1).
(2)∵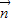 与
与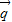 =(1,0)的夹角为
=(1,0)的夹角为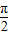 ,∴
,∴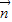 =(0,-1),
=(0,-1),
∴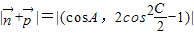 =|(cosA,cosC)|,
=|(cosA,cosC)|,
∴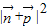 =cos2A+cos2C=
=cos2A+cos2C=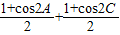
=1+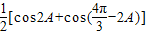 (∵A+C=
(∵A+C=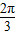 ,∴2C=
,∴2C=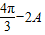 )
)
=1+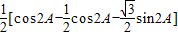
=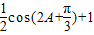 .
.
∵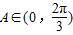 ,∴
,∴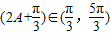 .
.
当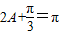 时,即A=
时,即A= 时,
时,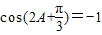 ,
,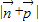 取得最小值,即
取得最小值,即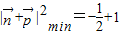 ,
,
∴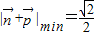 .
.
点评:熟练掌握向量和三角函数的运算及性质是解题的关键.
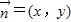 ,根据数量积的定义及坐标运算分别得出两个方程,解出即可;
,根据数量积的定义及坐标运算分别得出两个方程,解出即可;(2)根据向量的运算及三角运算得出
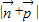 关于角A的三角表达式,再利用三角函数的单调性即可求出其最小值.
关于角A的三角表达式,再利用三角函数的单调性即可求出其最小值.解答:解:(1)设向量
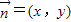 ,∵
,∵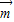 =(1,1),向量
=(1,1),向量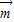 与
与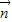 的夹角为
的夹角为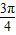 ,且
,且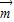 •
•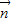 =-1.
=-1.∴
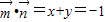 ,
,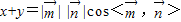 =
=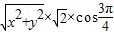 =-
=-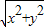 ,
,即
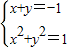 ,解得
,解得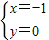 或
或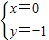 ,
,∴
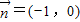 或(0,-1).
或(0,-1).(2)∵
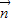 与
与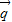 =(1,0)的夹角为
=(1,0)的夹角为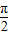 ,∴
,∴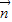 =(0,-1),
=(0,-1),∴
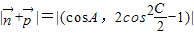 =|(cosA,cosC)|,
=|(cosA,cosC)|,∴
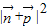 =cos2A+cos2C=
=cos2A+cos2C=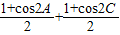
=1+
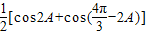 (∵A+C=
(∵A+C=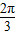 ,∴2C=
,∴2C=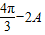 )
)=1+
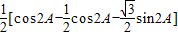
=
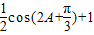 .
.∵
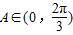 ,∴
,∴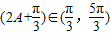 .
.当
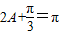 时,即A=
时,即A= 时,
时,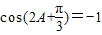 ,
,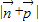 取得最小值,即
取得最小值,即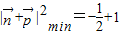 ,
,∴
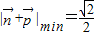 .
.点评:熟练掌握向量和三角函数的运算及性质是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知某海滨浴场的海浪高度y(单位:米)与时间 t(0≤t≤24)(单位:时)的函数关系记作y=f(t),下表是某日各时的浪高数据:
经长期观测,函数y=f(t)可近似地看成是函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T及函数表达 式(其中A>0,ω>0);
(2)根据规定,当海浪高度不低于0.75米时,才对冲浪爱好者开放,请根据以上结论,判断一天内从上午7时至晚上19时之间,该浴场有多少时间可向冲浪爱好者开放?
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T及函数表达 式(其中A>0,ω>0);
(2)根据规定,当海浪高度不低于0.75米时,才对冲浪爱好者开放,请根据以上结论,判断一天内从上午7时至晚上19时之间,该浴场有多少时间可向冲浪爱好者开放?