题目内容
等比数列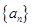 中,
中,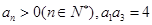 ,且
,且 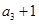 是
是  和
和 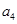 的等差中项,若
的等差中项,若 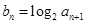
(Ⅰ)求数列  的通项公式;
的通项公式;
(Ⅱ)若数列  满足
满足 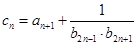 ,求数列
,求数列 的前n项和
的前n项和
(Ⅰ)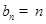 ;(Ⅱ)
;(Ⅱ)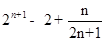
解析试题分析:(Ⅰ)由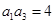 及等比数列性质可得
及等比数列性质可得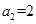 ,由
,由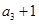 是
是  和
和 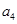 的等差中项知,
的等差中项知,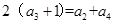 ,将上式用
,将上式用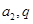 表示出来,化为关于公比
表示出来,化为关于公比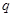 的方程,解出公比
的方程,解出公比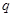 ,求出数列
,求出数列 的通项公式,代入
的通项公式,代入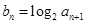 即可求出数列
即可求出数列 的通项公式;(Ⅱ)由(Ⅰ)
的通项公式;(Ⅱ)由(Ⅰ)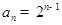 ,
,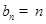 ,所以
,所以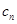 =
=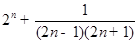 ,采用分组求和法求
,采用分组求和法求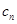 和,因为{
和,因为{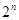 }是等比数列,用等比数列前n项和公式求和,对{
}是等比数列,用等比数列前n项和公式求和,对{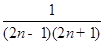 }用拆项相消法求和.
}用拆项相消法求和.
试题解析:(Ⅰ)由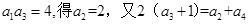 解得:
解得: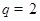
∴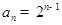 ∴
∴ 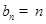 (6分)
(6分)
(Ⅱ)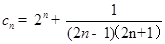 (8分)
(8分)
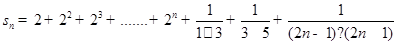
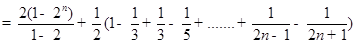
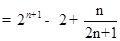 (12分)
(12分)
考点:等比数列通项公式、性质及前n项和公式,对数的运算法则,分组求和法,拆项相消法

练习册系列答案
相关题目
 ,该数列前n项和
,该数列前n项和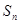 取最小值时,n = 。
取最小值时,n = 。 中,其中
中,其中 为数列
为数列 项和,并且
项和,并且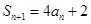 (
( ,
, .
.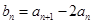 (
( 是等比数列;
是等比数列;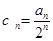 (
( 是等差数列;
是等差数列; 满足
满足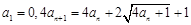 ,令
,令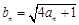 .
. 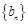 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;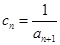 ,求
,求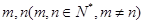 使得
使得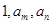 三数成等比数列?
三数成等比数列? 的公差为2,前
的公差为2,前 项和为
项和为 ,且
,且 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前 .
.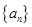 中,
中,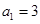 ,前
,前 项和
项和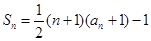 .
.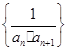 的前
的前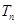 ,是否存在实数
,是否存在实数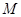 ,使得
,使得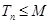 对一切正整数
对一切正整数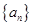 中,
中,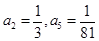
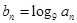 ,求数列
,求数列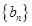 的前n项和
的前n项和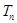 .
. 的前
的前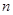 项和为
项和为 ,则
,则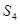 ,
,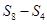 ,
,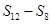 ,
,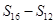 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列 的前
的前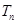 ,则
,则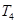 ,______,________
,______,________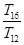 成等比数列.
成等比数列.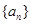 的前
的前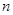 项和为
项和为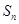 .若
.若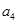 是
是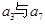 的等比中项,S10="60" ,则S20等于 _________
的等比中项,S10="60" ,则S20等于 _________