题目内容
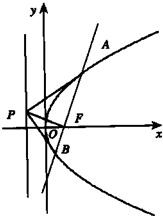 如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1),(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.
如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1),(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.(Ⅰ)求证:y1y2=-p2;
(Ⅱ)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;
(Ⅲ)若
| PA |
| PB |
分析:(I)(1)当直线AB的斜率不存在时,设直线AB的方程为:x=
,由此可知y1y2=-p2(1分)
(2)当直线AB的斜率存在且不为0时,设直线AB方程为:y=k(x-
),则由
,可得ky2-2py-kp2=0(k≠0)所以y1y2=-p2(3分)
(Ⅱ)由已知a=kPA,b=kPF,c=kPB,设P(-
,t),F(
,0),所以a=
,b=
,c=
;且x1=
,x2=
.由此入手可知a、b、c成等差数列.
(Ⅲ)由题意知a•c=-1,a-b=b-c.再由kAB的取值范围分别进行讨论,可以推导出θ=|α-β|.
| p |
| 2 |
(2)当直线AB的斜率存在且不为0时,设直线AB方程为:y=k(x-
| p |
| 2 |
|
(Ⅱ)由已知a=kPA,b=kPF,c=kPB,设P(-
| p |
| 2 |
| p |
| 2 |
| y1-t | ||
x1+
|
| -t |
| p |
| y2-t | ||
x2+
|
| ||
| 2p |
| ||
| 2p |
(Ⅲ)由题意知a•c=-1,a-b=b-c.再由kAB的取值范围分别进行讨论,可以推导出θ=|α-β|.
解答:证明:(I)(1)当直线AB的斜率不存在时,设直线AB的方程为:x=
,
则A(
,p),B(
,-p),∴y1y2=-p2(1分)
(2)当直线AB的斜率存在且不为0时,设直线AB方程为:y=k(x-
),
则由
,可得ky2-2py-kp2=0(k≠0)∴y1y2=-p2(3分)
(Ⅱ)由已知a=kPA,b=kPF,c=kPB,
设P(-
,t),F(
,0)∴a=
,b=
,c=
;且x1=
,x2=
故a+c=
+
=
+
=
+
=2p•
=2p•
=2p•
=-
=2b
∴a、b、c成等差数列(8分)
(Ⅲ)∵
⊥
=0
∴PA⊥PB,故a•c=-1
由(Ⅱ)可知a+c=2b,即a-b=b-c
①若AB⊥x轴,则α=β=45°,θ=0°∴θ=α-β
②若kAB>0,则tanα=
=
=
=
=-c
同理可得tanβ=α
∴tan(α-β)=
=
=-
=-b
即|tan(α-β)|=|b|=tanθ
易知∠PFO,∠BPF,∠APF都是锐角∴θ=|α-β|
③若kAB<0,类似的也可证明θ=|α-β|
总上所述,θ=|α-β|(14分)
| p |
| 2 |
则A(
| p |
| 2 |
| p |
| 2 |
(2)当直线AB的斜率存在且不为0时,设直线AB方程为:y=k(x-
| p |
| 2 |
则由
|
(Ⅱ)由已知a=kPA,b=kPF,c=kPB,
设P(-
| p |
| 2 |
| p |
| 2 |
| y1-t | ||
x1+
|
| -t |
| p |
| y2-t | ||
x2+
|
| ||
| 2p |
| ||
| 2p |
故a+c=
| y1-t | ||
x1+
|
| y2-t | ||
x2+
|
| y1-t | ||||||
|
| y2-t | ||||||
|
| 2p(y1-t) | ||
|
| 2p(y2-t) | ||
|
=2p•
(y1-t)(
| ||||
(
|
=2p•
y1
| ||||||||
|
=2p•
-t(
| ||||
p2(
|
=-
| 2t |
| p |
∴a、b、c成等差数列(8分)
(Ⅲ)∵
| PA |
| PB |
∴PA⊥PB,故a•c=-1
由(Ⅱ)可知a+c=2b,即a-b=b-c
①若AB⊥x轴,则α=β=45°,θ=0°∴θ=α-β
②若kAB>0,则tanα=
| a-b |
| 1+ab |
| a-b |
| -ac+ab |
| a-b |
| a(b-c) |
| 1 |
| a |
同理可得tanβ=α
∴tan(α-β)=
| tanα-tanβ |
| 1+tanα•tanβ |
| -c-a |
| 1+(-c)a |
| a+c |
| 2 |
即|tan(α-β)|=|b|=tanθ
易知∠PFO,∠BPF,∠APF都是锐角∴θ=|α-β|
③若kAB<0,类似的也可证明θ=|α-β|
总上所述,θ=|α-β|(14分)
点评:本题考查圆锥曲线的位置关系,解题时要认真审题,结合图形效果会更好.

练习册系列答案
相关题目
 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=

 .
.