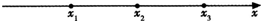题目内容
在一条直线型的工艺流水线上有3个工作台，将工艺流水线用如图2-19所示的数轴表示，各工作台的坐标分别为x1，x2，x3，每个工作台上有若干名工人．现要在x1与x3之间修建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短．
（1）若每个工作台上只有一名工人，试确定供应站的位置；
（2）设从左到右工作台上的工人人数依次为2，1，3，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值．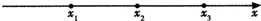
（1）若每个工作台上只有一名工人，试确定供应站的位置；
（2）设从左到右工作台上的工人人数依次为2，1，3，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值．
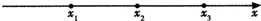
分析：（1）设供应站坐标为x，各工作台上的所有工人到供应站的距离之和为d（x），由题意有d（x）=|x-x1|+|x-x2|+|x-x3|，然后对x的范围进行讨论分析，知当x=x2时，所有工人到供应站的距离之和最短．
（2）由题设知，各工作台上的所有工人到供应站的距离之和为d（x）=2|x-x1|+|x-x2|+3|x-x3|，类似（1）的讨论，即可得到结论．
（2）由题设知，各工作台上的所有工人到供应站的距离之和为d（x）=2|x-x1|+|x-x2|+3|x-x3|，类似（1）的讨论，即可得到结论．
解答：解：设供应站坐标为x，各工作台上的所有工人到供应站的距离之和为d（x）．
（1）d（x）=|x-x1|+|x-x2|+|x-x3|．
当x＜x1时，d（x）=x1+x2+x3-3x在区间（-∞，x1）上是减函数；
当x＞x3时，d（x）=3x-（x1+x2+x3）在区间（x3，+∞）上是增函数；
所以，x必须位于区间[x1，x3]内，此时d（x）=x3-x1+|x-x2|（*），
当且仅当x=x2时，（*）式取最小值，且d（x2）=x3-x1，即供应站的位置为x=x2；
（2）由题设知，各工作台上的所有工人到供应站的距离之和为d（x）=2|x-x1|+|x-x2|+3|x-x3|
当x＜x1时，d（x）=2x1+x2+3x3-6x在区间（-∞，x1）上是减函数；
当x1＜x＜x2时，d（x）=-2x1+x2+3x3-2x在区间（x1，x2）上是减函数；
当x2＜x＜x3时，d（x）=-2x1-x2+3x3在区间（x2，x3）上是常数函数
当x＞x3时，d（x）=6x-（2x1+x2+3x3）在区间（x3，+∞）上是增函数；
所以，x必须位于区间[x2，x3]内，此时d（x）取最小值．
（1）d（x）=|x-x1|+|x-x2|+|x-x3|．
当x＜x1时，d（x）=x1+x2+x3-3x在区间（-∞，x1）上是减函数；
当x＞x3时，d（x）=3x-（x1+x2+x3）在区间（x3，+∞）上是增函数；
所以，x必须位于区间[x1，x3]内，此时d（x）=x3-x1+|x-x2|（*），
当且仅当x=x2时，（*）式取最小值，且d（x2）=x3-x1，即供应站的位置为x=x2；
（2）由题设知，各工作台上的所有工人到供应站的距离之和为d（x）=2|x-x1|+|x-x2|+3|x-x3|
当x＜x1时，d（x）=2x1+x2+3x3-6x在区间（-∞，x1）上是减函数；
当x1＜x＜x2时，d（x）=-2x1+x2+3x3-2x在区间（x1，x2）上是减函数；
当x2＜x＜x3时，d（x）=-2x1-x2+3x3在区间（x2，x3）上是常数函数
当x＞x3时，d（x）=6x-（2x1+x2+3x3）在区间（x3，+∞）上是增函数；
所以，x必须位于区间[x2，x3]内，此时d（x）取最小值．
点评：本题主要考查将实际问题转化为数学问题的能力，以及综合运用函数知识解决问题的能力，解题的关键是分类去绝对值号．
练习册系列答案
相关题目
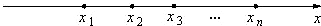
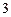个工作台，将工艺流水线用如图
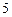所示的数轴表示，各工作台的坐标分别为
，
，
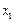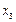，每个工作台上有若干名工人．现要在
，
，
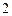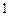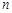个工作台，将工艺流水线用如图
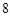所示的数轴表示，各工作台的坐标分别为
，
，
，
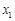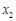，每个工作台上有若干名工人．现要在流水线上建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短．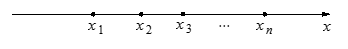
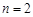，每个工作台上只有一名工人，试确定供应站的位置；
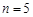，工作台从左到右的人数依次为
，
，
，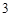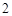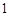