题目内容
已知向量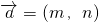 ,
,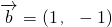 ,其中m,n为连续两次投掷骰子得到的点数,则
,其中m,n为连续两次投掷骰子得到的点数,则 的夹角能成为直角三角形的内角的概率是________.
的夹角能成为直角三角形的内角的概率是________.

分析:由已知中m,n为连续两次投掷骰子得到的点数,我们可以列举出(m,n)的所有情况,并列举出
 的夹角能成为直角三角形的内角的基本事件个数,代入古典概型概率计算公式,即可得到答案.
的夹角能成为直角三角形的内角的基本事件个数,代入古典概型概率计算公式,即可得到答案.解答:连续两次投掷骰子得到的点数(m,n)共有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共36个
若
 的夹角能成为直角三角形的内角,则m≥n
的夹角能成为直角三角形的内角,则m≥n共有(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),
(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),
(5,3),(5,4),(5,5),(6,1),(6,2),(6,3),
(6,4),(6,5),(6,6).共21个
故
 的夹角能成为直角三角形的内角的概率P=
的夹角能成为直角三角形的内角的概率P=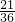 =
=
故答案为:

点评:本题考查的知识点是数量积表示两个向量的夹角,等可能事件的概率,在解答时要注意
 的夹角能成为直角三角形的内角,是指
的夹角能成为直角三角形的内角,是指 的夹角不大于90°,本题易将此点理解为
的夹角不大于90°,本题易将此点理解为 的夹角为直角,而错解为
的夹角为直角,而错解为 .
. 
练习册系列答案
相关题目
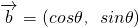 ,其中m,n,θ∈R.若
,其中m,n,θ∈R.若 ,则当
,则当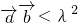 恒成立时实数λ的取值范围是
恒成立时实数λ的取值范围是 或
或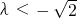
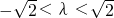
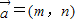 ,
,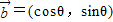 ,其中m,n,θ∈R.若
,其中m,n,θ∈R.若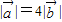 ,则当
,则当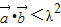 恒成立时实数λ的取值范围是( )
恒成立时实数λ的取值范围是( )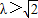 或
或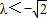
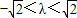
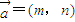 ,
,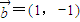 ,其中m,n为连续两次投掷骰子得到的点数,则
,其中m,n为连续两次投掷骰子得到的点数,则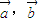 的夹角能成为直角三角形的内角的概率是 .
的夹角能成为直角三角形的内角的概率是 .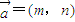 ,
,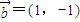 ,其中m,n∈{1,2,3,4,5},则
,其中m,n∈{1,2,3,4,5},则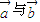 的夹角能成为直角三角形内角的概率是 .
的夹角能成为直角三角形内角的概率是 .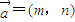 ,
,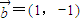 ,其中m,n为连续两次投掷骰子得到的点数,则
,其中m,n为连续两次投掷骰子得到的点数,则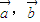 的夹角能成为直角三角形的内角的概率是 .
的夹角能成为直角三角形的内角的概率是 .