题目内容
商家通常依据“乐观系数准则”确定商品销售价格，及根据商品的最低销售限价a，最高销售限价b（b＞a）以及常数x（0＜x＜1）确定实际销售价格c=a+x（b-a），这里，x被称为乐观系数．
经验表明，最佳乐观系数x恰好使得（c-a）是（b-c）和（b-a）的等比中项，据此可得，最佳乐观系数x的值等于________．
分析：根据题设条件，由（c-a）是（b-c）和（b-a）的等比中项，知[x（b-a）]2=（b-a）2-x（b-a）2，由此能求出最佳乐观系数x的值．
解答：∵c-a=x（b-a），b-c=（b-a）-x（b-a），
（c-a）是（b-c）和（b-a）的等比中项，
∴[x（b-a）]2=（b-a）2-x（b-a）2，
∴x2+x-1=0，
解得
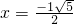，∵0＜x＜1，
∴
．故答案为：
．点评：本题考查等比数列的性质和应用，解题时要注意等比中项的计算．
练习册系列答案
阅读快车系列答案
相关题目
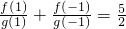，则a的值为________．
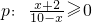，命题q：x2-2x+1-m2≤0（m＜0），且p是q的必要条件，求实数m的范围．
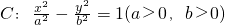的焦距为4，且过点（2，3），则它的渐近线方程为________．