题目内容
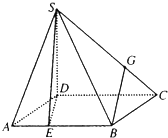 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= ,点E、G分别在AB、SC上,且
,点E、G分别在AB、SC上,且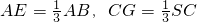 .
.
(1)证明:BC∥平面SDE;(2)求面SAD与面SBC所成二面角的大小.
证明:(1)在SD上取点F,使SF= SD,连接FG,FE,
SD,连接FG,FE,
由CG= SC,得FG∥CD,且FG=
SC,得FG∥CD,且FG= CD
CD
又AE= AB,得BE∥CD,且BE=
AB,得BE∥CD,且BE= CD
CD
∴FG=BE,FG∥BE
∴BG∥FE
∵FE?平面SDE,BG?平面SDE
∴BG∥平面SDE…5分
(2)连接BD,在正方形ABCD中,BC=3,∴BD=3
∵SD丄底面ABCD,
∴SD⊥BD,又SB= ,
,
∴SD=3…6分
又平面SAD⊥平面ABCD,平面SCD⊥平面ABCD,
∴BC⊥SC,BA⊥平面SAD,CD⊥平面SAD
设平面SAD与平面ABC所成的二面角的平面角为θ…9分
则cosθ=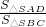 =
=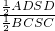 =
=
∴θ=
即平面SAD与平面ABC所成的二面角的平面角为 …12分
…12分
分析:(1)在SD上取点F,使SF= SD,连接FG,FE,由已知条件结合平行线分线段成比例定理,我们可证得BG∥FE,进而根据线面平行的判定定理即可得到BC∥平面SDE;
SD,连接FG,FE,由已知条件结合平行线分线段成比例定理,我们可证得BG∥FE,进而根据线面平行的判定定理即可得到BC∥平面SDE;
(2)连接BD,由已知中SD丄底面ABCD,可得平面SAD⊥平面ABCD,由面面垂直的性质可得△SBC在平面SAD上的投影即为△SAD,则cosθ=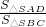 ,分别求出两个三角形的面积即可得到面SAD与面SBC所成二面角的大小.
,分别求出两个三角形的面积即可得到面SAD与面SBC所成二面角的大小.
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,其中(1)的关键是证得BG∥FE,(2)的关键是证得△SBC在平面SAD上的投影即为△SAD,则cosθ=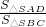 .
.
 SD,连接FG,FE,
SD,连接FG,FE,由CG=
 SC,得FG∥CD,且FG=
SC,得FG∥CD,且FG= CD
CD又AE=
 AB,得BE∥CD,且BE=
AB,得BE∥CD,且BE= CD
CD∴FG=BE,FG∥BE
∴BG∥FE
∵FE?平面SDE,BG?平面SDE
∴BG∥平面SDE…5分
(2)连接BD,在正方形ABCD中,BC=3,∴BD=3
∵SD丄底面ABCD,
∴SD⊥BD,又SB=
 ,
,∴SD=3…6分
又平面SAD⊥平面ABCD,平面SCD⊥平面ABCD,
∴BC⊥SC,BA⊥平面SAD,CD⊥平面SAD
设平面SAD与平面ABC所成的二面角的平面角为θ…9分
则cosθ=
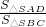 =
=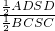 =
=
∴θ=

即平面SAD与平面ABC所成的二面角的平面角为
 …12分
…12分分析:(1)在SD上取点F,使SF=
 SD,连接FG,FE,由已知条件结合平行线分线段成比例定理,我们可证得BG∥FE,进而根据线面平行的判定定理即可得到BC∥平面SDE;
SD,连接FG,FE,由已知条件结合平行线分线段成比例定理,我们可证得BG∥FE,进而根据线面平行的判定定理即可得到BC∥平面SDE;(2)连接BD,由已知中SD丄底面ABCD,可得平面SAD⊥平面ABCD,由面面垂直的性质可得△SBC在平面SAD上的投影即为△SAD,则cosθ=
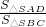 ,分别求出两个三角形的面积即可得到面SAD与面SBC所成二面角的大小.
,分别求出两个三角形的面积即可得到面SAD与面SBC所成二面角的大小.点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,其中(1)的关键是证得BG∥FE,(2)的关键是证得△SBC在平面SAD上的投影即为△SAD,则cosθ=
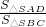 .
. 
练习册系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.