题目内容
下列命题中:
①一个整数的平方是偶数,则这个整数是偶数;
②
是无理数;
③经过平面内一点和平面外一点的直线一定不在平面内;
④若向量
、
是平面向量的一组基底,则
+
与
-
也可作为平面向量的一组基底.
其中正确的命题是
①一个整数的平方是偶数,则这个整数是偶数;
②
| 2 |
③经过平面内一点和平面外一点的直线一定不在平面内;
④若向量
| a |
| b |
| a |
| b |
| a |
| b |
其中正确的命题是
①②③④
①②③④
.分析:用反证法证明,①④为正确命题;
根据直线在平面内,直线上的所有点都在平面内判断③是否正确.
根据直线在平面内,直线上的所有点都在平面内判断③是否正确.
解答:解:∵设这个数不是偶数,则(2n+1)2=4n2+4n+1=2(2n2+2n)+1=2m+1.(m=2n2+2n),它的平方不是偶数,∴假设错误,①正确;
是无理数,∴②正确;
∵直线在平面内,直线上的所有点都在平面内,过平面内一点和平面外一点的直线一定不在平面内,③正确;
设
+
与
-
共线,则
+
=λ(
-
)⇒
=
,
与
共线,∴
+
与
-
不共线,可作为平面向量的一组基底,④正确.
故答案是①②③④
| 2 |
∵直线在平面内,直线上的所有点都在平面内,过平面内一点和平面外一点的直线一定不在平面内,③正确;
设
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| λ+1 |
| λ-1 |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故答案是①②③④
点评:本题考查命题的真假判断.反证法是证明的常用方法,其证明的思路是:首先假设与要证明的结论相反的结论成立,
然后从假设的结论出发,推导出与已知的矛盾(或明显的不成立),否定假设的结论,从而证明要证的结论成立.
然后从假设的结论出发,推导出与已知的矛盾(或明显的不成立),否定假设的结论,从而证明要证的结论成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是( )
中至少有一个是偶数时,下列假设中正确的是( )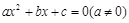 有有理根,那么
有有理根,那么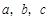 中至少有一个是偶数时,下列假设中正确的是( )
中至少有一个是偶数时,下列假设中正确的是( ) 有有
有有  中至少有一个是偶数”时,下列假设中正确的是(
)
中至少有一个是偶数”时,下列假设中正确的是(
) 有有理数根,
有有理数根, 、
、 、
、 中至少有一个是偶数时,下列假设中正确的是( )
中至少有一个是偶数时,下列假设中正确的是( )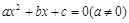 有有理根,那么
有有理根,那么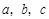 中至少有一个是偶数。”下列假设中正确的是( )
中至少有一个是偶数。”下列假设中正确的是( )