Question

14.设平面内有ｎ条直线，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用表示这ｎ条直线交点的个数，则＝_____________；当ｎ＞４时，＝_____________．（用n表示）

Answer 1

14. 5,  .

解析：同一平面内两条直线若不平行则一定相交，故每增加一条直线一定与前面已有的每条直线都相交，

∴f（k）=f（k－1）+（k－1）.

如图，当n=3时，只有两个交点，

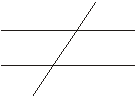
即f（3）=2，

f（4）=f（3）+3=2+3；

f（5）=f（4）+4=2+3+4；

……

f（k）=f（k－1）+（k－1）=2+3+4+…+（k－1），

∴f（k）=（k+1）（k－2）.

∴f（n）=（n－2）（n+1）.

或利用f（k）－f（k－1）=k－1，

则f（4）－f（3）=3，

f（5）－f（4）=4，

……

f（n）－f（n－1）=n－1，

将上面n－4式子相加得f（n）－f（3）=3+4+…+（n－1），

∴f（n）=（n－2）（n+1）.