Question

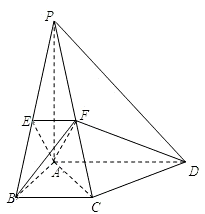如图，在四棱锥P-ABCD中，平面PAC⊥平面ABCD，且PA⊥AC，PA=AD=2．四边形ABCD满足BC∥AD，AB⊥AD，AB=BC=1．点E，F分别为侧棱PB，PC上的点，且．
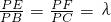（Ⅰ）求证：EF∥平面PAD；
（Ⅱ）当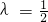时，求异面直线BF与CD所成角的余弦值；
（Ⅲ）是否存在实数λ，使得平面AFD⊥平面PCD？若存在，试求出λ的值；若不存在，请说明理由．

Answer 1

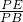证明：（Ⅰ）由已知，==λ，
所以EF∥BC．
因为BC∥AD，所以EF∥AD．
而EF?平面PAD，AD?平面PAD，
所以EF∥平面PAD． …（4分）
（Ⅱ）因为平面ABCD⊥平面PAC，
平面ABCD∩平面PAC=AC，且PA⊥AC，
所以PA⊥平面ABCD．
所以PA⊥AB，PA⊥AD．
又因为AB⊥AD，
所以PA，AB，AD两两垂直． …（5分）
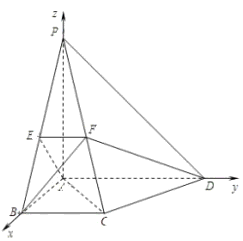
如图所示，建立空间直角坐标系，
因为AB=BC=1，PA=AD=2，
所以A（0，0，0），B（1，0，0），C（1，1，0），D（0，2，0），P（0，0，2）．
当λ=时，F为PC中点，
所以F（，，1），
所以=（-，，1），=（-1，1，0）．
设异面直线BF与CD所成的角为θ，
所以cosθ=|cos＜，＞|==，
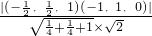所以异面直线BF与CD所成角的余弦值为．…（9分）
（Ⅲ）设F（x₀，y₀，z₀），则=（x₀，y₀，z₀-2），=（1，1，-2）．
由已知=λ，所以（x₀，y₀，z₀-2）=λ（1，1，-2），
所以，
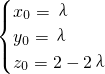∴=（λ，λ，2-2λ）．
设平面AFD的一个法向量为n₁=（x₁，y₁，z₁），因为=（0，2，0），
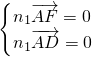所以即，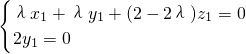
令z₁=λ，得n₁=（2λ-2，0，λ）．
设平面PCD的一个法向量为n₂=（x₂，y₂，z₂），
因为=（0，2，-2），=（-1，1，0），
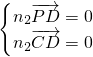所以即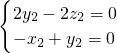
令x₂=1，则n₂=（1，1，1）．
若平面AFD⊥平面PCD，则n₁•n₂=0，所以（2λ-2）+λ=0，解得．
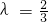所以当λ=时，平面AFD⊥平面PCD．…（14分）
分析：（Ⅰ）由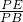==λ可知，EF∥BC，依题意，可求得EF∥AD，再利用线面平行的判断定理即可证得结论；
（Ⅱ）可证得PA，AB，AD两两垂直，以之为轴建立空间直角坐标系，可求得与的坐标，利用向量的数量积即可求得异面直线BF与CD所成角的余弦值；
（Ⅲ）设F（x₀，y₀，z₀），则=（x₀，y₀，z₀-2），=（1，1，-2），由=λ，可求得F（λ，λ，2-2λ），再设出平面AFD的一个法向量为n₁=（x₁，y₁，z₁），平面PCD的一个法向量为n₂=（x₂，y₂，z₂），可求得这两个法向量的坐标，利用n₁•n₂=0，即可求得λ的值．
点评：本题考查直线与平面的平行，考查异面直线所成的角，考查面面垂直，突出考查空间直角坐标系在证明与计算中的应用．属于中档题．