题目内容
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使得当x∈[a,b]时,f(x)的值域是[a,b],则称函数f(x)为“M函数”.给出下列四个函数:
①f(x)=x+1 ②f(x)=-x2+1
③f(x)=2x-2 ④f(x)=
-
其中所有“M函数”的序号是( )
①f(x)=x+1 ②f(x)=-x2+1
③f(x)=2x-2 ④f(x)=
| x |
| 1 |
| 8 |
其中所有“M函数”的序号是( )
分析:根据定义域求出值域,然后寻找其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b]的a与b的值,即可判定.
解答: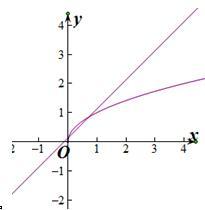 解:(1)①f(x)=x+1当x∈[a,b]时,f(x)的值域是[a+1,b+1],找不到满足条件的a与b,根据定义可知f(x)=x+1不是“M函数”
解:(1)①f(x)=x+1当x∈[a,b]时,f(x)的值域是[a+1,b+1],找不到满足条件的a与b,根据定义可知f(x)=x+1不是“M函数”
②f(x)=-x2+1,当x∈[0,1]时,f(x)的值域是[0,1],根据定义可知f(x)=-x2+1是“M函数”;
③f(x)=2x-2,由于它在R上是增函数,当x∈[a,b]时,f(x)的值域是[2a-2,2b-2],
由2a-2=a,2b-2=b,得2a=a+2,2b=b+2,由图象可知,函数y=2x与y=x+2有两个交点,
根据定义可知f(x)=2x-2是“M函数”;
④f(x)=
-
,由于它在R上是增函数,当x∈[a,b]时,f(x)的值域是[
-
,
-
],
由a=
-
,b=
-
,得
=a+
,
=b+
,由图象可知,函数y=
与y=x+
有两个交点,
根据定义可知f(x)=
-
是“M函数”;
故所有“M函数”的序号是:②③④.
故选D.
 解:(1)①f(x)=x+1当x∈[a,b]时,f(x)的值域是[a+1,b+1],找不到满足条件的a与b,根据定义可知f(x)=x+1不是“M函数”
解:(1)①f(x)=x+1当x∈[a,b]时,f(x)的值域是[a+1,b+1],找不到满足条件的a与b,根据定义可知f(x)=x+1不是“M函数”②f(x)=-x2+1,当x∈[0,1]时,f(x)的值域是[0,1],根据定义可知f(x)=-x2+1是“M函数”;
③f(x)=2x-2,由于它在R上是增函数,当x∈[a,b]时,f(x)的值域是[2a-2,2b-2],
由2a-2=a,2b-2=b,得2a=a+2,2b=b+2,由图象可知,函数y=2x与y=x+2有两个交点,
根据定义可知f(x)=2x-2是“M函数”;
④f(x)=
| x |
| 1 |
| 8 |
| a |
| 1 |
| 8 |
| b |
| 1 |
| 8 |
由a=
| a |
| 1 |
| 8 |
| b |
| 1 |
| 8 |
| a |
| 1 |
| 8 |
| b |
| 1 |
| 8 |
| x |
| 1 |
| 8 |
根据定义可知f(x)=
| x |
| 1 |
| 8 |
故所有“M函数”的序号是:②③④.
故选D.
点评:本题主要考查了函数与方程的综合运用,解题的关键是将原问题转化为方程的解,进而转化为函数图象的交点问题,利用数形结合的思想方法加以解决,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目