题目内容
设函数f(x)=x3+ax,g(x)=2x2+b,已知它们的图象在x=1处有相同的切线.(Ⅰ)求函数f(x)和g(x)的解析式;
(Ⅱ)若函数F(x)=f(x)-m•g(x)在区间[
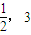 ]上是单调减函数,求实数m的取值范围.
]上是单调减函数,求实数m的取值范围.
【答案】分析:(I)欲求函数f(x)和g(x)的解析式利用在点x=1处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率,利用斜率相等列出等式.从而求出a,b.
(Ⅱ)由于F(x)=f(x)-mg(x)=x3+x-2mx2,求出其导数得F'(x)=3x2-4mx+1,原问题等价于3x2-4mx+1≤0在区间[ ]上恒成立,最后利用二次函数的图象与性质解决即得.
]上恒成立,最后利用二次函数的图象与性质解决即得.
解答:解:(I)f'(x)=3x2+a,g'(x)=4x
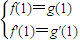 ,
,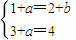
∴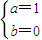
∴f(x)=x3+x,g(x)=2x2
(Ⅱ)∵F(x)=f(x)-mg(x)=x3+x-2mx2
∴F'(x)=3x2-4mx+1若x∈[ ,3]时,F(x)是减函数,
,3]时,F(x)是减函数,
则3x2-4mx+1≤0恒成立,
得
∴ .
.
实数m的取值范围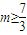 .
.
点评:本小题主要考查函数解析式的求解及待定系数法、导数的几何意义、利用导数研究曲线上某点切线方程、利用导数研究函数的单调性等基础知识,考查运算求解能力.属于基础题.
(Ⅱ)由于F(x)=f(x)-mg(x)=x3+x-2mx2,求出其导数得F'(x)=3x2-4mx+1,原问题等价于3x2-4mx+1≤0在区间[
 ]上恒成立,最后利用二次函数的图象与性质解决即得.
]上恒成立,最后利用二次函数的图象与性质解决即得.解答:解:(I)f'(x)=3x2+a,g'(x)=4x
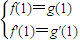 ,
,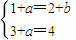
∴
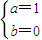
∴f(x)=x3+x,g(x)=2x2
(Ⅱ)∵F(x)=f(x)-mg(x)=x3+x-2mx2
∴F'(x)=3x2-4mx+1若x∈[
 ,3]时,F(x)是减函数,
,3]时,F(x)是减函数,则3x2-4mx+1≤0恒成立,
得

∴
 .
.实数m的取值范围
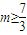 .
.点评:本小题主要考查函数解析式的求解及待定系数法、导数的几何意义、利用导数研究曲线上某点切线方程、利用导数研究函数的单调性等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目