题目内容
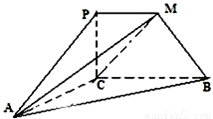
如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.①求证:平面PAC⊥平面ABC;
②求三棱锥A-MBC的体积.
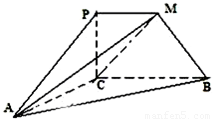
【答案】分析:①由∠PCB=90°,得PC⊥CB,又AB⊥PC,利用线面垂直的判定可以证明PC⊥平面ABC,继而得到面面垂直;
②由PC⊥平面ABC,根据面面垂直的判定可得面ABC⊥面PVBM,再由两面垂直的性质定理可得三棱锥A-MBC的高,解直角三角形求出三棱锥A-MBC的高,则体积可求.
解答:①证明:∵∠PCB=90°,∴PC⊥CB,又PC⊥AB,且AB∩BC=B,∴PC⊥平面ABC,又PC?平面PAC,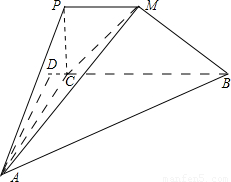
∴平面PAC⊥平面ABC;
②∵PC⊥平面ABC,PC?平面PCBM,∴平面PCBM⊥平面ABC,
如图,
在平面ABC中过A作AD垂直于BC的延长线与D,则AD⊥平面PCBM,则AD为三棱锥A-MBC的高,
∵∠ACB=120°,∴∠ACD=60°,在直角三角形ADC中,AD=ACsin60°=1×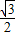 =
=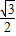 .
.
又S△BMC=S四边形PCBM-S△MPC=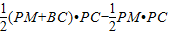 =
=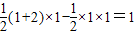 .
.
∴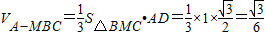 .
.
所以,三棱锥A-MBC的体积为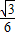 .
.
点评:本题主要考查了直线与平面、平面与平面垂直的判定和性质,考查空间想象能力、运算能力和推理论证能力,属于中档题.
②由PC⊥平面ABC,根据面面垂直的判定可得面ABC⊥面PVBM,再由两面垂直的性质定理可得三棱锥A-MBC的高,解直角三角形求出三棱锥A-MBC的高,则体积可求.
解答:①证明:∵∠PCB=90°,∴PC⊥CB,又PC⊥AB,且AB∩BC=B,∴PC⊥平面ABC,又PC?平面PAC,

∴平面PAC⊥平面ABC;
②∵PC⊥平面ABC,PC?平面PCBM,∴平面PCBM⊥平面ABC,
如图,
在平面ABC中过A作AD垂直于BC的延长线与D,则AD⊥平面PCBM,则AD为三棱锥A-MBC的高,
∵∠ACB=120°,∴∠ACD=60°,在直角三角形ADC中,AD=ACsin60°=1×
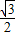 =
=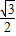 .
.又S△BMC=S四边形PCBM-S△MPC=
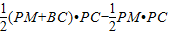 =
=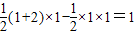 .
.∴
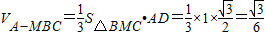 .
.所以,三棱锥A-MBC的体积为
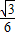 .
.点评:本题主要考查了直线与平面、平面与平面垂直的判定和性质,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.
如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.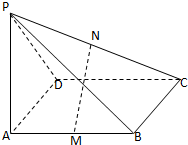 如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,
如图所示,四边形ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB,PC的中点,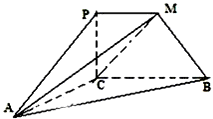 如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.
如图所示,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,∠ACB=120°,AB⊥PC.