题目内容
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率.
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(2)试估计生活垃圾投放错误的概率.
分析:(1)由题意和概率的定义易得所求概率;
(2)设生活垃圾投放错误为事件A,则其对立事件
表示生活垃圾投放正确,先求P(
),由对立事件的关系可得答案.
(2)设生活垃圾投放错误为事件A,则其对立事件
. |
| A |
. |
| A |
解答:解:(1)由题意结合概率的定义可得:厨余垃圾投放正确的概率为:
=
=
;
(2)设生活垃圾投放错误为事件A,则其对立事件
表示生活垃圾投放正确.
事件
的概率约为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量
与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,
即P(
)=
=0.7.
所以P(A)=1-0.7=0,3.
| “厨余垃圾”箱里厨余垃圾量 |
| 厨余垃圾总量 |
| 400 |
| 400+100+100 |
| 2 |
| 3 |
(2)设生活垃圾投放错误为事件A,则其对立事件
. |
| A |
事件
. |
| A |
与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,
即P(
. |
| A |
| 400+240+60 |
| 1000 |
所以P(A)=1-0.7=0,3.
点评:本题考查古典概型的求解和对立事件,属基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
|
|
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
厨余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为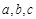 ,其中
,其中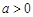 ,
,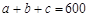 。当数据
。当数据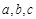 的方差
的方差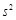 最大时,写出
最大时,写出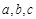 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时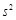 的值.
的值.
(注: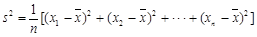 ,其中
,其中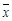 为数据
为数据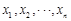 的平均数)
的平均数)
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(2)试估计生活垃圾投放错误的概率.
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率.
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(2)试估计生活垃圾投放错误的概率.
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率.
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(2)试估计生活垃圾投放错误的概率.