题目内容
已知二次函数f(x)=x2-2x+6,设向量a=(sinx,2),b=(2sinx, ),c=(cos2x,1),d=(1,2).当x∈[0,π]时,不等式f>f的解集为 .
),c=(cos2x,1),d=(1,2).当x∈[0,π]时,不等式f>f的解集为 .
【答案】分析:由已知中二次函数f(x)=x2-2x+6,根据二次函数的图象和性质,我们可以分析出f(x)在(1,+∞)内单调递增,由向量数量积公式,及已经中各向量的坐标,我们易判断出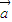 •
•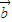 ≥1,
≥1,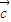 •
•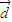 ≥1,进而将f(
≥1,进而将f(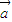 •
•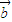 )>f(
)>f(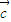 •
•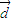 )可化为
)可化为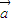 •
•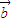 >
>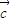 •
•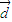 ,结合三角函数的性质及x∈[0,π],可求出不等式的解集.
,结合三角函数的性质及x∈[0,π],可求出不等式的解集.
解答:解:∵二次函数f(x)=x2-2x+6,
∴f(x)图象关于x=1对称,
∴f(x)在(1,+∞)内单调递增.
又∵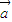 •
•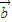 =2sin2x+1≥1,
=2sin2x+1≥1, •
• =cos2x+1≥1,
=cos2x+1≥1,
则f(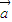 •
•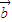 )>f(
)>f(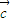 •
•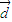 )可化为
)可化为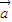 •
•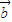 >
>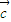 •
•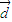 ,
,
即2sin2x+1>2cos2x+1,
又∵x∈[0,π],
∴x∈(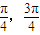 ).
).
故不等式的解集为(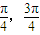 ).
).
故答案为:(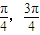 ).
).
点评:本题考查的知识点是一元二次不等式的应用,二次函数的图象和性质,平面向量的数量积公式,三角函数的图象和性质,其中根据二次函数的图象和性质分析出f(x)在(1,+∞)内单调递增进而将f(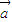 •
•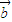 )>f(
)>f(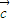 •
•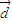 )可化为
)可化为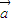 •
•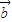 >
>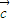 •
•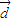 是解答本题的关键.
是解答本题的关键.
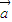 •
•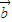 ≥1,
≥1,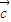 •
•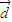 ≥1,进而将f(
≥1,进而将f(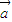 •
•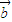 )>f(
)>f(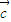 •
•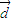 )可化为
)可化为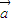 •
•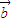 >
>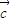 •
•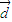 ,结合三角函数的性质及x∈[0,π],可求出不等式的解集.
,结合三角函数的性质及x∈[0,π],可求出不等式的解集.解答:解:∵二次函数f(x)=x2-2x+6,
∴f(x)图象关于x=1对称,
∴f(x)在(1,+∞)内单调递增.
又∵
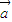 •
•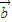 =2sin2x+1≥1,
=2sin2x+1≥1, •
• =cos2x+1≥1,
=cos2x+1≥1,则f(
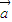 •
•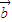 )>f(
)>f(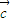 •
•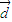 )可化为
)可化为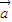 •
•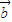 >
>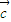 •
•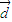 ,
,即2sin2x+1>2cos2x+1,
又∵x∈[0,π],
∴x∈(
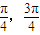 ).
).故不等式的解集为(
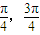 ).
).故答案为:(
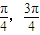 ).
).点评:本题考查的知识点是一元二次不等式的应用,二次函数的图象和性质,平面向量的数量积公式,三角函数的图象和性质,其中根据二次函数的图象和性质分析出f(x)在(1,+∞)内单调递增进而将f(
 •
• )>f(
)>f(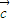 •
•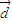 )可化为
)可化为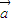 •
•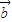 >
>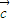 •
•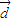 是解答本题的关键.
是解答本题的关键. 
练习册系列答案
相关题目