题目内容
四棱锥P-ABCD中,底面ABCD是矩形,又PA=PD,E是BC的中点.(1)求证:AD⊥PE;
(2)在PA上是否存在一点M,使ME∥平面PDC?
【答案】分析:(1)取AD的中点O,连接OP,OE,由PA=PD,结合等腰三角形“三线合一”的性质,可得OP⊥AD,又由矩形中位线的性质,可得OE⊥AD,进而根据线面垂直的判定定理,可得AD⊥平面OPE,再由线面垂直的性质即可得到AD⊥PE;
(2)PA的中点M,连接ME,MO,根据三角形中线定理,我们可得OM∥PD,又由OE∥DC,结合面面平行的判定定理,可得平面OEM∥平面PDC,进而由面面平行的性质,得到结论.
解答: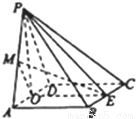 解:(1)如图,取AD的中点O,连接OP,OE
解:(1)如图,取AD的中点O,连接OP,OE
∵PA=PD,∴OP⊥AD,
又E是BC的中点,∴OE∥AB,∴OE⊥AD,
又OP∩OE=O,∴AD⊥平面OPE,而PE?平面OPE,
∴AD⊥PE.
(2)存在点M,取PA的中点M,
连接ME,MO,易知:OM∥PD,又由OE∥DC,
知:平面OEM∥平面PDC.
故在PA上是否存在点M(M为PA的中点),使ME∥平面PDC.
点评:本题考查的知识眯是直线与平面平行的判定,直线与平面垂直的判定与性质,熟练掌握空间直线与平面平行、垂直的判定定理,性质定理,定义及相互的转化,是解答此类问题的关键.
(2)PA的中点M,连接ME,MO,根据三角形中线定理,我们可得OM∥PD,又由OE∥DC,结合面面平行的判定定理,可得平面OEM∥平面PDC,进而由面面平行的性质,得到结论.
解答:
 解:(1)如图,取AD的中点O,连接OP,OE
解:(1)如图,取AD的中点O,连接OP,OE∵PA=PD,∴OP⊥AD,
又E是BC的中点,∴OE∥AB,∴OE⊥AD,
又OP∩OE=O,∴AD⊥平面OPE,而PE?平面OPE,
∴AD⊥PE.
(2)存在点M,取PA的中点M,
连接ME,MO,易知:OM∥PD,又由OE∥DC,
知:平面OEM∥平面PDC.
故在PA上是否存在点M(M为PA的中点),使ME∥平面PDC.
点评:本题考查的知识眯是直线与平面平行的判定,直线与平面垂直的判定与性质,熟练掌握空间直线与平面平行、垂直的判定定理,性质定理,定义及相互的转化,是解答此类问题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
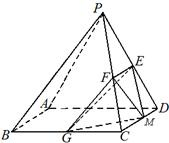 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.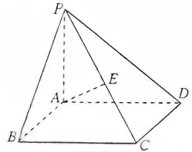 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2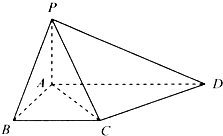 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.