Question

设sinθ、cosθ是方程4x²-4mx+2m-1=0的两个根, ＜θ＜2π,求m和θ的值.

Answer 1

思路分析：由sinθ、cosθ是方程的两根，根据一元二次方程根与系数的关系得到关于sinθ、cosθ的方程组，化归为已知三角函数值求角，利用给定角的范围，准确求角.

解：由条件知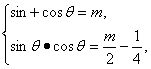

    而(sinθ+cosθ)²=sin²θ+cos²θ+2sinθ·cosθ.

∴m²=1+m-.

∴m=1±.

∵＜θ＜2π,

∴sinθ·cosθ=＜0.

∴m＜.

∴m=1-.

    易知方程的两根为和-,

    又∵＜θ＜2π,

∴sinθ=-且cosθ=.

∴θ=.