题目内容
已知函数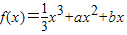 的极大值点为x=-1.
的极大值点为x=-1.(Ⅰ)用实数a来表示实数b,并求a的取值范围;
(Ⅱ)当x∈[-1,2]时,f(x)的最小值为
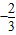 ,求a的值;
,求a的值;(Ⅲ)设A(-1,f(-1)),B(2,f(2)),A,B两点的连线斜率为k.求证:必存在x∈(-1,2),使f′(x)=k.
【答案】分析:(I)求出导函数,令导函数在极值点x=-1出的值为0,得到a,b的关系;利用导函数的韦达定理求出另一个极值点,据x=-1是极大值得到两个极值点的大小关系,列出不等式求出a的范围.
(II)据(I)得到函数的单调性,通过极值点1-2a与区间端点位置关系的讨论,求出函数的最小值,列出方程求出a的值.
(III)利用两点连线的斜率公式求出k,令f′(x)=k有解,通过二次方程的实根分布,得到证明.
解答:解:(Ⅰ)f′(x)=x2+2ax+b,由题设知f′(-1)=0
∴b=2a-1
韦达定理得另一极值点x=-b=1-2a,因为x=-1为极大值点
故1-2a>-1,
∴a<1
(Ⅱ)f(x)在(-∞,-1)上递增,在(-1,1-2a)递减,在(1-2a,+∞)上递增,
故当x∈[-1,2]时,分情况如下:
①1-2a≥2,即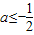 时,f(x)在x∈[-1,2]上单调递减
时,f(x)在x∈[-1,2]上单调递减
∴ ,
,
解得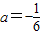 ,不合条件,舍去
,不合条件,舍去
②1-2a<2,即 时,
时,
∴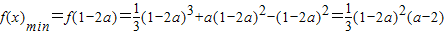
∴ ,化简得a(2a-3)2=0,a=0或
,化简得a(2a-3)2=0,a=0或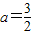 ,取a=0
,取a=0
综上,故所求的a=0
(Ⅲ) ,即证x2+2ax+b=3a
,即证x2+2ax+b=3a
即证方程x2+2ax-a-1=0(a<1)在x∈(-1,2)上有实数解
记g(x)=x2+2ax-a-1=0(a<1),
g(-1)=-3a,g(2)=3a+3
①当g(-1)•g(2)=-3a(a+1)<0,即a<-1或0<a<1时,由零点存在定理知此时方程有解
②a<0时,此时△=4(a2+a+1)>0,g(2)>0,g(-1)>0,且二次函数g(x)的
对称轴x=-a∈(0,1)⊆(-1,2),由此可知此时方程在(-1,2)内有两个解
③a=-1时方程有一根为x=0,当a=0时方程有一根为x=1
综上可知,方程x2+2ax-a-1=0(a<1)在x∈(-1,2)上有实数解.
即必存在x∈(-1,2),使f'(x)=k.
点评:导函数在极值点处的值为0;解决二次方程实根分布问题常从判别式、对称轴与区间端点值的符号、区间端点值的符号几方面考虑.
(II)据(I)得到函数的单调性,通过极值点1-2a与区间端点位置关系的讨论,求出函数的最小值,列出方程求出a的值.
(III)利用两点连线的斜率公式求出k,令f′(x)=k有解,通过二次方程的实根分布,得到证明.
解答:解:(Ⅰ)f′(x)=x2+2ax+b,由题设知f′(-1)=0
∴b=2a-1
韦达定理得另一极值点x=-b=1-2a,因为x=-1为极大值点
故1-2a>-1,
∴a<1
(Ⅱ)f(x)在(-∞,-1)上递增,在(-1,1-2a)递减,在(1-2a,+∞)上递增,
故当x∈[-1,2]时,分情况如下:
①1-2a≥2,即
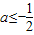 时,f(x)在x∈[-1,2]上单调递减
时,f(x)在x∈[-1,2]上单调递减∴
 ,
,解得
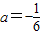 ,不合条件,舍去
,不合条件,舍去②1-2a<2,即
 时,
时,∴
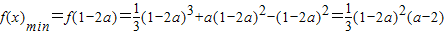
∴
 ,化简得a(2a-3)2=0,a=0或
,化简得a(2a-3)2=0,a=0或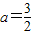 ,取a=0
,取a=0综上,故所求的a=0
(Ⅲ)
 ,即证x2+2ax+b=3a
,即证x2+2ax+b=3a即证方程x2+2ax-a-1=0(a<1)在x∈(-1,2)上有实数解
记g(x)=x2+2ax-a-1=0(a<1),
g(-1)=-3a,g(2)=3a+3
①当g(-1)•g(2)=-3a(a+1)<0,即a<-1或0<a<1时,由零点存在定理知此时方程有解
②a<0时,此时△=4(a2+a+1)>0,g(2)>0,g(-1)>0,且二次函数g(x)的
对称轴x=-a∈(0,1)⊆(-1,2),由此可知此时方程在(-1,2)内有两个解
③a=-1时方程有一根为x=0,当a=0时方程有一根为x=1
综上可知,方程x2+2ax-a-1=0(a<1)在x∈(-1,2)上有实数解.
即必存在x∈(-1,2),使f'(x)=k.
点评:导函数在极值点处的值为0;解决二次方程实根分布问题常从判别式、对称轴与区间端点值的符号、区间端点值的符号几方面考虑.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
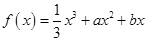 的极大值点为
的极大值点为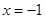 .
.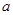 来表示实数
来表示实数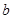 ,并求
,并求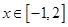 时,
时,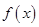 的最小值为
的最小值为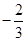 ,求
,求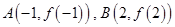 ,
,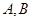 两点的连线斜率为
两点的连线斜率为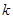 .求证:必存在
.求证:必存在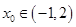 ,使
,使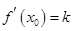 .
.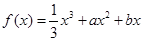 的极大值点为
的极大值点为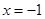 ,
,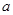 来表示实数
来表示实数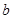 ,并求
,并求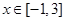 时,若
时,若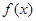 的最大值为6,求实数
的最大值为6,求实数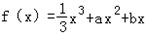 的极大值点为x=﹣1.
的极大值点为x=﹣1.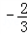 ,求a的值;
,求a的值;