题目内容

设集合A={（x，y）|y≥|x-2|，x≥0}，B={（x，y）|y≤-x+b}，若A∩B≠∅，（x，y）∈A∩B，且x+2y的最大值为9，则b的值是______．
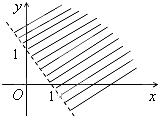
如图：集合A={（x，y）|y≥|x-2|，x≥0}表示图中阴影部分，
集合B={（x，y）|y≤-x+b}表示直线y=-x+b的下方，
∵A∩B≠∅．
若（x，y）∈A∩B，令z=x+2y
作直线z=x+2y，由图知当直线过（0，b）时，z最大
所以0+2b=9，解得b=
9
2
．
故答案为：
9
2

练习册系列答案
相关题目
不等式组
(x-y+1)(x+y-1)≥0
-2≤x≤2
表示平面区域的面积为______．
已知实数x，y满足条件
x-y+2≥0
0≤x≤3
y≥0
，则目标函数z=2x-y的最大值是______．
已知点P在△ABC内（包括边界），且
AP
=λ
AB
+μ
AC
，若对于满足条件的λ和μ，都有|aλ+bμ|≤2成立，则动点Q（a，b）形成的平面区域的面积（　　）
A．8B．16C．32D．64
设x，y满足约束条件
x≥0
x+2y≥4
2x+y≤5
，则z=2x-y的最大值是______．
如果实数xy满足不等式组
x-y+1≤0，x≥1
2x-y-2≤0
，则x2+y2的最小值是______．
桂林市某商场为使销售空调和冰箱获得的总利润达到最大，对即将出售的空调和冰箱相关数据进行调查，得出下表：
资金每台空调或冰箱所需资金（百元）月资金供应数量 （百元）
空调冰箱
成本3020300
工人工资510110
每台利润68
问：该商场怎样确定空调或冰箱的月供应量，才能使总利润最大？
图中阴影部分表示的平面区域满足的不等式是（　　）
A．x+y-1＜0B．x+y-1＞0C．x-y-1＜0D．x-y-1＞0
若a≥0，b≥0，且当
x≥0
y≥0
x+y≤1
时，恒有ax+by≤1，则以a、b为坐标的点P（a，b）所形成的平面区域的面积等于______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网