题目内容
在△ABC中,已知tanA=
,tanB=
,若△ABC最长边的长为1,则最短边的长为______.
| 1 |
| 2 |
| 1 |
| 3 |
∵tan45°=1,tanA=
,tanB=
,
∴tanB<tanA<tan45°,即B<A<45°,AC为最短边,
∴△ABC最大角为钝角C,最长边的长为AB=1,
根据题意画出图形,过C作CD⊥AB,交AB于点D,
由tanA=
=
,tanB=
=
,即AD=2CD,DB=3CD,
∴AB=AD+DB=5DC=1,即CD=
,
∵tanA=
,
∴cosA=
=
,sinA=
=
,
利用正弦定理得:
=
,即AC=
=
.
故答案为:

| 1 |
| 2 |
| 1 |
| 3 |
∴tanB<tanA<tan45°,即B<A<45°,AC为最短边,
∴△ABC最大角为钝角C,最长边的长为AB=1,
根据题意画出图形,过C作CD⊥AB,交AB于点D,
由tanA=
| CD |
| AD |
| 1 |
| 2 |
| CD |
| DB |
| 1 |
| 3 |
∴AB=AD+DB=5DC=1,即CD=
| 1 |
| 5 |
∵tanA=
| 1 |
| 2 |
∴cosA=
|
2
| ||
| 5 |
| 1-cos2A |
| ||
| 5 |
利用正弦定理得:
| AC |
| sin∠ADC |
| CD |
| sinA |
| ||||
|
| ||
| 5 |
故答案为:
| ||
| 5 |


练习册系列答案
相关题目
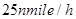 、
、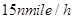 ,则下午2时两船之间的距离是_______nmile。
,则下午2时两船之间的距离是_______nmile。