题目内容
下列函数中是偶函数的是
A.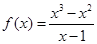 | B.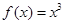 | C.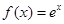 | D.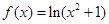 |
D
解析试题分析:选项A中,由于定义域x 1,定义域不能关于原点对称,故是非奇非偶函数;
1,定义域不能关于原点对称,故是非奇非偶函数;
选项B中,定义域为R,且有f(-x)=-x3=-f(x)=x3,故函数为奇函数,选项C中,由于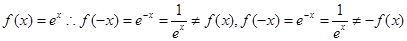 因此是非奇非偶函数,
因此是非奇非偶函数,
选项D中,由于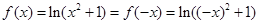 ,定义域为R,是偶函数,故选D.
,定义域为R,是偶函数,故选D.
考点:本试题主要考查了函数的奇偶性的概念的运用。
点评:解决该试题的关键是理解奇偶性的判定,要看两步:首先看定义域是否关于原点对称,你然后看f(-x)与f(x)的关系式即可。

练习册系列答案
相关题目
函数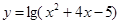 的单调递增区间为( )
的单调递增区间为( )
A.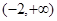 | B.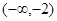 | C.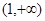 | D.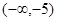 |
下列各组函数中,f(x)与g(x)表示同一函数的是( )
A.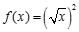 与 与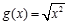 | B.f(x)=x与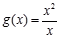 |
C.f(x)=x与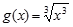 | D.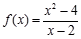 与g(x)=x+2 与g(x)=x+2 |
设函数 上单调递增,则
上单调递增,则 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
已知函数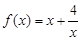 ,且当
,且当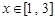 ,
,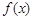 的值域是
的值域是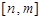 ,则
,则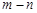 的值是
的值是
A.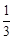 | B.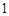 | C. | D.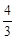 |
设f(x)是R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=
| A.1 | B.3 | C.-1 | D.-3 |
函数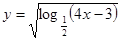 的定义域为 ( )
的定义域为 ( )
A.(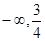 ) ) | B.(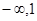 ] ] | C.(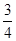 ,1] ,1] | D.(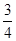 ,1) ,1) |
如果两个函数的对应关系相同,值域相同,但定义域不同,则这两个函数为“同族函数”,那么函数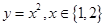 的“同族函数”有( )
的“同族函数”有( )
| A.3个 | B.7个 | C.8个 | D.9个 |
 ,定义运算
,定义运算 ,其中
,其中 是常数,等式右边的运算是通常的加法和乘法运算.已知
是常数,等式右边的运算是通常的加法和乘法运算.已知 ,并且有一个非零常数
,并且有一个非零常数 ,使得对任意实数
,使得对任意实数 ,都有
,都有 ,则
,则


