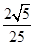题目内容
若α,β均为锐角,sinα= ,cos(α+β)=
,cos(α+β)= ,则cosβ=( )
,则cosβ=( )A.
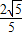
B.

C.
 或
或
D.

【答案】分析:由同角三角函数的基本关系,结合α、β均为锐角算出sin(α+β)= 且cosα=
且cosα=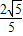 ,再由两角差的余弦公式结合配角,即可算出cosβ的值.
,再由两角差的余弦公式结合配角,即可算出cosβ的值.
解答:解:∵α,β均为锐角,sinα=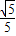 ,cos(α+β)=
,cos(α+β)= ,
,
∴sin(α+β)=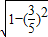 =
= ,cosα=
,cosα=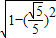 =
=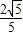
可得cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα= ×
×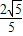 +
+ ×
×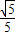 =
=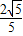 ,
,
故选:A
点评:本题通过求特殊的三角函数值,着重考查了同角三角函数的基本关系、两角和与差的三角函数公式等知识,考查了配角的思路,属于中档题.
 且cosα=
且cosα=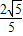 ,再由两角差的余弦公式结合配角,即可算出cosβ的值.
,再由两角差的余弦公式结合配角,即可算出cosβ的值.解答:解:∵α,β均为锐角,sinα=
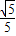 ,cos(α+β)=
,cos(α+β)= ,
,∴sin(α+β)=
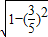 =
= ,cosα=
,cosα=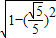 =
=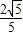
可得cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=
 ×
×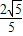 +
+ ×
×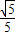 =
=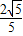 ,
,故选:A
点评:本题通过求特殊的三角函数值,着重考查了同角三角函数的基本关系、两角和与差的三角函数公式等知识,考查了配角的思路,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,sin(α+β)=
,sin(α+β)= ,则cosβ等于( )
,则cosβ等于( )