题目内容
设数列 的前n项和为
的前n项和为 ,已知
,已知 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令
 .用数学归纳法证明:
.用数学归纳法证明:
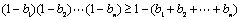 ;
;
(3)设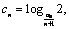 数列
数列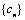 的前n项和为
的前n项和为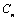 ,若存在整数m,使对任意
,若存在整数m,使对任意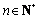 且
且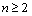 ,都有
,都有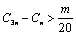 成立,求m的最大值.
成立,求m的最大值.
【答案】
(1)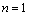 时,
时,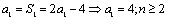 时,
时,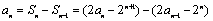
 .故
.故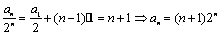 (5分)
(5分)
(2)由(1)知: ,原不等式即证
,原不等式即证

①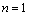 时,
时,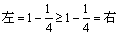 ,故
,故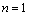 成立;
成立;
②假设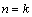 时,
时,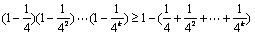 ,
,
则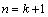 时,
时,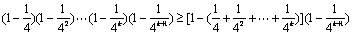
=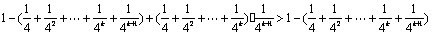
故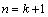 也成立;综合①、②知原不等式恒成立. (10分)
也成立;综合①、②知原不等式恒成立. (10分)
(3)由(1)知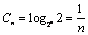 ,令
,令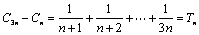 ,
,
则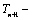
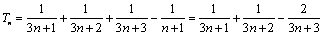
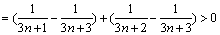
故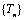 为单增数列,且
为单增数列,且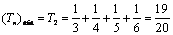 .
.
原不等式恒成立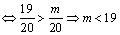 ,又
,又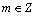 ,故
,故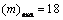 . (14分)
. (14分)

练习册系列答案
相关题目
 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,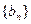 为等比数列,且
为等比数列,且 (Ⅰ)求数列
(Ⅰ)求数列 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.