题目内容
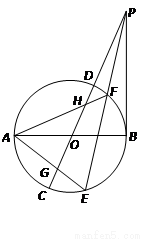
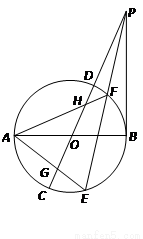
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H
(Ⅰ)设EF中点为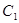 ,求证:O、
,求证:O、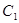 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
【答案】
(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
试题分析:利用对角互补得到四点共圆,利用相似得到边长相等.
试题解析:证明:(Ⅰ)
易知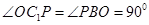 ,
,
所以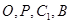 四点共圆. 3分
四点共圆. 3分
(Ⅱ)由(Ⅰ) 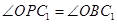
过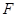 作
作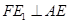 于
于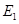 ,交
,交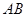 于
于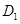
连结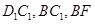
由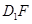 ∥
∥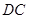 ,
, 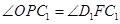
所以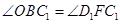
所以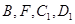 四点共圆. 6分
四点共圆. 6分
所以 ,由此
,由此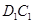 ∥
∥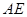 ,
8分
,
8分
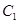 是
是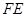 的中点,
的中点,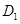 是
是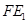 的中点,所以
的中点,所以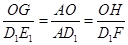 ,所以OG =OH 10分
,所以OG =OH 10分
考点:四点共圆证明;相似证明.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
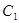 ,求证:O、
,求证:O、
 ,求证:O、
,求证:O、 (Ⅰ)设EF中点为
(Ⅰ)设EF中点为