题目内容
已知抛物线C: , 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
⑴若抛物线C在点M的法线的斜率为 ,求点M的坐标
,求点M的坐标 ;
;
⑵设P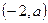 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
 , 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。⑴若抛物线C在点M的法线的斜率为
 ,求点M的坐标
,求点M的坐标 ;
;⑵设P
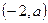 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。(1)(
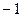 ,
,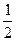 )
)(2)略
解:
⑴函数 的导数
的导数 ,点
,点 处切线的斜率k0=
处切线的斜率k0=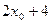
.∵过点 的法线斜率为
的法线斜率为 ,∴
,∴ (
(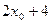 )=
)=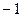 ,解得
,解得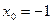 ,
,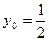 。
。
故点M的坐标为(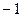 ,
,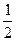 )。
)。
⑵设M 为C上一点,
为C上一点,
若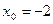 ,则C上点M
,则C上点M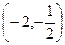 处的切线斜率k=0,
处的切线斜率k=0,
过点M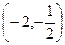 的法线方程为
的法线方程为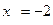 ,次法线过点P
,次法线过点P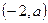 ;
;
若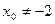 ,则过点M
,则过点M 的法线方程为:
的法线方程为: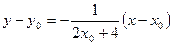 。
。
若法线过点P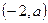 ,则
,则 ,即
,即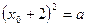 。
。
若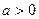 ,则
,则 ,从而
,从而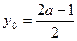 ,
,
代入得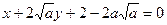 ,
,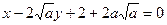 。
。
若 ,与
,与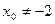 矛盾,若
矛盾,若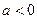 ,则无解。
,则无解。
综上,当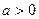 时,在C上有三点(
时,在C上有三点( ,
, ),(
),(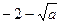 ,
, )及
)及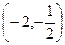 ,
,
在该点的法线通过点P,
法线方程分别为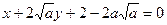 ,
,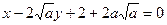 ,
,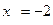 。
。
当
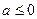 时,在C上有一点
时,在C上有一点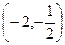 ,在该点的法线通过点P,法线方程为
,在该点的法线通过点P,法线方程为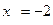 。
。
⑴函数
 的导数
的导数 ,点
,点 处切线的斜率k0=
处切线的斜率k0=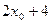
.∵过点
 的法线斜率为
的法线斜率为 ,∴
,∴ (
(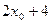 )=
)=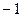 ,解得
,解得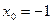 ,
,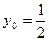 。
。故点M的坐标为(
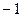 ,
,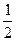 )。
)。⑵设M
 为C上一点,
为C上一点,若
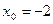 ,则C上点M
,则C上点M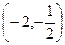 处的切线斜率k=0,
处的切线斜率k=0,过点M
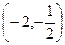 的法线方程为
的法线方程为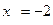 ,次法线过点P
,次法线过点P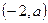 ;
;若
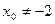 ,则过点M
,则过点M 的法线方程为:
的法线方程为: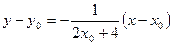 。
。若法线过点P
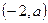 ,则
,则 ,即
,即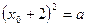 。
。若
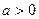 ,则
,则 ,从而
,从而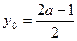 ,
,代入得
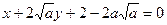 ,
,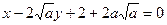 。
。若
 ,与
,与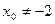 矛盾,若
矛盾,若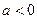 ,则无解。
,则无解。综上,当
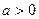 时,在C上有三点(
时,在C上有三点( ,
, ),(
),(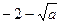 ,
, )及
)及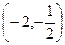 ,
,在该点的法线通过点P,
法线方程分别为
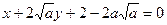 ,
,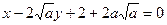 ,
,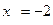 。
。当

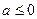 时,在C上有一点
时,在C上有一点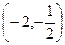 ,在该点的法线通过点P,法线方程为
,在该点的法线通过点P,法线方程为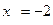 。
。
练习册系列答案
相关题目
 、
、 ,则∠
,则∠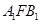 =( )
=( )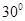 B.
B. 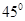 C.
C. 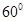 D.
D. 
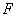 为抛物线
为抛物线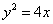 的焦点,
的焦点,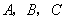 为该抛物线上三点,若
为该抛物线上三点,若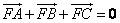 ,则
,则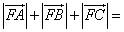
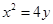 上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )
上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( ) 、
、 、
、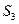 ,试判断S
,试判断S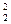 =4
=4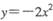 的焦点坐标是
的焦点坐标是
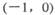

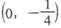
 2x-y=4距离最近的点的坐标是( )
2x-y=4距离最近的点的坐标是( )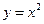 和直线
和直线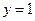 所围成图形的面积为______________
所围成图形的面积为______________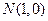 ,动点
,动点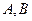
 分别在抛物线
分别在抛物线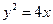 及曲线
及曲线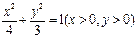 上,若
上,若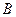 在
在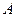 的右侧,且
的右侧,且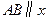 轴,则
轴,则
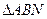 的周长
的周长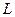 的取值范围是
的取值范围是