题目内容
已知函数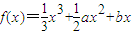 的两个极值点x1,x2,若x1∈(-∞,-1].x2∈[2,+∞),则a+b的最大值是( )
的两个极值点x1,x2,若x1∈(-∞,-1].x2∈[2,+∞),则a+b的最大值是( )A.-5
B.-3
C.1
D.3
【答案】分析:由题意得x1,x2,为f′(x)的两个零点,且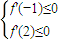 ,利用线性规划知识即可求得a+b的最大值.
,利用线性规划知识即可求得a+b的最大值.
解答:解:f′(x)=x2+ax+b,由题意知x1,x2,为f′(x)的两个零点,
且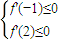 ,即
,即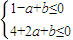 ,
,
作出满足不等式组的点(a,b)构成的区域如图阴影所示:
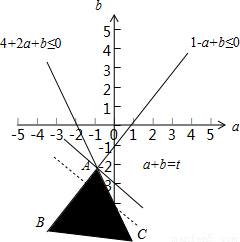
令t=a+b,由图知当直线t=a+b经过点A时t最大,由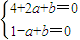 解得A(-1,-2),
解得A(-1,-2),
tmax=-1-2=-3,即a+b的最大值为-3.
故选B.
点评:本题考查利用导数研究函数的极值问题,考查线性规划知识,考查学生综合运用知识解决问题的能力.
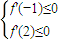 ,利用线性规划知识即可求得a+b的最大值.
,利用线性规划知识即可求得a+b的最大值.解答:解:f′(x)=x2+ax+b,由题意知x1,x2,为f′(x)的两个零点,
且
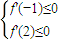 ,即
,即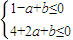 ,
,作出满足不等式组的点(a,b)构成的区域如图阴影所示:

令t=a+b,由图知当直线t=a+b经过点A时t最大,由
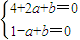 解得A(-1,-2),
解得A(-1,-2),tmax=-1-2=-3,即a+b的最大值为-3.
故选B.
点评:本题考查利用导数研究函数的极值问题,考查线性规划知识,考查学生综合运用知识解决问题的能力.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
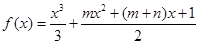 的两个极值点分别为
的两个极值点分别为 ,且
,且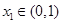 ,
,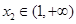 ,点
,点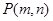 表示的平面区域为
表示的平面区域为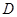 ,若函数
,若函数 的图象上存在区域
的图象上存在区域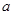 的取值范围为
.
的取值范围为
. 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
, ,点
,点 表示的平面区域为
表示的平面区域为 ,若函数
,若函数 的图像上存在区域
的图像上存在区域 的取值范围是( )
的取值范围是( ) B.
B.
 C.
C. D.
D.
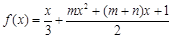 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
,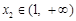 ,点
,点 表示的平面区域为
表示的平面区域为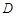 ,若函数
,若函数 的图像上存在区域
的图像上存在区域 B.
B.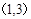 C.
C. D.
D.
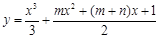 的两个极值点分别为x1,x2,且x1Î(0,
1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0,
1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数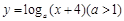 的图象上存在区域D内的点,则实数a的取值范围为(
)
的图象上存在区域D内的点,则实数a的取值范围为(
) 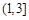 B.
B.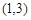 C.
C.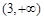 D.
D.