题目内容
为了考察某种大麦穗长的分布情况,在一块试验地里抽取了100个穗,量得它们的长度如下(单位:厘米):6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0
5.4 4.6 5.8 5.5 6.0 6.5 5.1 6.5
5.3 5.9 5.5 5.8 6.2 5.4 5.0 5.0
6.8 6.0 5.0 5.7 6.0 5.5 6.8 6.0
6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4
5.7 7.4 6.0 5.4 6.5 6.0 6.8 5.8
6.3 6.0 6.3 5.6 5.3 6.4 5.7 6.7
6.2 5.6 6.0 6.7 6.7 6.0 5.5 6.2
6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0
5.2 6.0 6.3 5.7 6.8 6.1 4.5 5.6
6.3 6.0 5.8 6.3
列出样本的频率分布表,画出频率分布直方图.
分析:总体中个体取不同数值较多甚至无限时,对其频率分布的研究要用到初中学过的整理样本数据的知识和初中《统计初步》中画频率分布直方图的步骤.
解:(1)计算最大值与最小值的差.在样本数据中,最大值7.4,最小值4.0.它们的差7.4-4.0=3.4(厘米).
(2)决定组距与组数.
在本例中,最大值与最小值的差是3.4厘米,如果取组距为0.3厘米,那么由于![]() =11
=11![]() 得分成12组,组数合适.于是取定组距为0.3厘米,组数为12.
得分成12组,组数合适.于是取定组距为0.3厘米,组数为12.
(3)决定分点.
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点,那么,所分的12个小组可以是:3.95—4.25,4.25—4.55,4.55—4.85,…,7.25—7.55.
(4)列频率分布表.
对各个小组作频数累计,然后数频数,算频率,列频率分布表,如下表所示.
频率分布表
分组 | 频数累计 | 频数 | 频率 |
3.95—4.25 | 一 | 1 | 0.01 |
4.25—4.55 | 一 | 1 | 0.01 |
4.55—4.85 |
| 2 | 0.02 |
4.85—5.15 | 正 | 5 | 0.05 |
5.15—5.45 | 正正一 | 11 | 0.11 |
5.45—5.75 | 正正正 | 15 | 0.15 |
5.75—6.05 | 正正正正正 | 28 | 0.28 |
6.05—6.35 | 正正 | 13 | 0.13 |
6.35—6.65 | 正正一 | 11 | 0.11 |
6.65—6.95 | 正正 | 10 | 0.10 |
6.95—7.25 |
| 2 | 0.02 |
7.25—7.55 | 一 | 1 | 0.01 |
合计 |
| 100 | 1.00 |
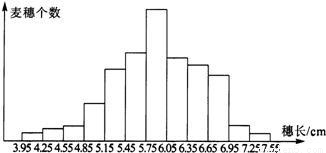
(5)画频率分布直方图
从表和图中看到,长度在5.75—6.05厘米的麦穗所占的比最大,达到28%,而长度在3.95—4.25、4.25—4.55、4.55—4.85、6.95—7.25、7.25—7.55等范围内的麦穗所占的比的和只有7%.
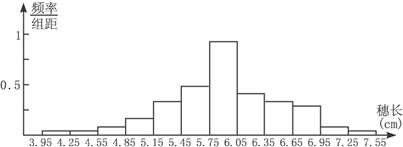

 12、为了考察某种大麦穗长的分布情况,在一块试验地里抽取了100个穗,量得它们的长度(单位:cm)之后,将所得数据以0.3cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出的频数分布直方图如图,由图可知( )
12、为了考察某种大麦穗长的分布情况,在一块试验地里抽取了100个穗,量得它们的长度(单位:cm)之后,将所得数据以0.3cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出的频数分布直方图如图,由图可知( )