题目内容
函数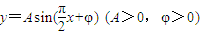 的部分图象如图所示,设P是图象的
的部分图象如图所示,设P是图象的一个最高点,M,N是图象与x轴的交点,若tan∠MPN=-2,则A= .
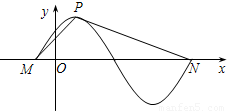
【答案】分析:依题意,可求得y=Asin(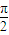 x+φ)(A>0,φ>0)的周期T=4=MN,设点P在x轴上的射影为Q,tan∠MPQ=
x+φ)(A>0,φ>0)的周期T=4=MN,设点P在x轴上的射影为Q,tan∠MPQ=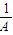 ,tan∠NPQ=
,tan∠NPQ=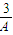 ,利用∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,即可求得A.
,利用∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,即可求得A.
解答:解:∵y=Asin(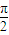 x+φ)的周期T=
x+φ)的周期T=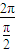 =4,由图知,MN=T=4,
=4,由图知,MN=T=4,
又P是图象的一个最高点,设点P在x轴上的射影为Q,则MQ= T=1,QN=
T=1,QN= T=3,
T=3,
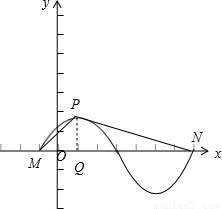
∴tan∠MPQ=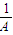 ,tan∠NPQ=
,tan∠NPQ=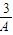 ,
,
∵∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,
∴tan(∠MPQ+∠NPQ)=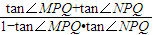 =
=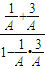 =-2,
=-2,
∴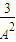 -
-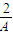 -1=0,即(
-1=0,即( -1)(
-1)(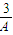 +1)=0,又A>0,
+1)=0,又A>0,
∴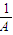 =1,A=1.
=1,A=1.
故答案为:1.
点评:本题考查y=Asin(ωx+φ)的图象与性质,考查两角和的正切,考查正弦函数的周期与最值的应用,属于中档题.
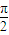 x+φ)(A>0,φ>0)的周期T=4=MN,设点P在x轴上的射影为Q,tan∠MPQ=
x+φ)(A>0,φ>0)的周期T=4=MN,设点P在x轴上的射影为Q,tan∠MPQ=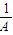 ,tan∠NPQ=
,tan∠NPQ=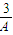 ,利用∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,即可求得A.
,利用∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,即可求得A.解答:解:∵y=Asin(
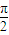 x+φ)的周期T=
x+φ)的周期T=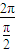 =4,由图知,MN=T=4,
=4,由图知,MN=T=4,又P是图象的一个最高点,设点P在x轴上的射影为Q,则MQ=
 T=1,QN=
T=1,QN= T=3,
T=3,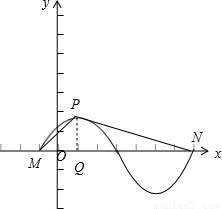
∴tan∠MPQ=
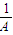 ,tan∠NPQ=
,tan∠NPQ=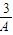 ,
,∵∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,
∴tan(∠MPQ+∠NPQ)=
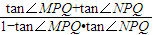 =
=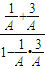 =-2,
=-2,∴
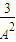 -
-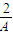 -1=0,即(
-1=0,即( -1)(
-1)(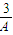 +1)=0,又A>0,
+1)=0,又A>0,∴
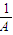 =1,A=1.
=1,A=1.故答案为:1.
点评:本题考查y=Asin(ωx+φ)的图象与性质,考查两角和的正切,考查正弦函数的周期与最值的应用,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( ) 已知函数f(x)是(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( ) (2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4
(2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4 (2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
(2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( ) 函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,该函数的部分图象如图所示,A、B分别为最高点与最低点,并且
函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,该函数的部分图象如图所示,A、B分别为最高点与最低点,并且