题目内容
在极坐标系中,从极点O作直线与另一直线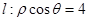 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使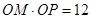 .
.
(1)求点P的轨迹方程; (2)设R为
(2)设R为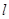 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值.
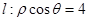 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使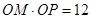 .
.(1)求点P的轨迹方程;
 (2)设R为
(2)设R为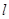 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值.解:(1)设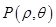 ,
,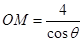 ,因为
,因为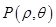 在直线OM上,
在直线OM上,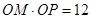 ,所以
,所以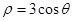
(2)由直线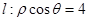 和P的轨迹
和P的轨迹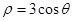 ,由此可知RP的最小值为1.
,由此可知RP的最小值为1.
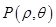 ,
,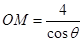 ,因为
,因为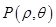 在直线OM上,
在直线OM上,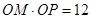 ,所以
,所以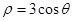
(2)由直线
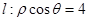 和P的轨迹
和P的轨迹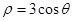 ,由此可知RP的最小值为1.
,由此可知RP的最小值为1. 考查学生综合运用直线与圆方程解决数学问题的能力,以及会求简单曲线的极坐标方程.
(1)设动点P的坐标为(ρ,θ),M的坐标为(ρ0,θ),则ρρ0=12,由ρ0cosθ=4,得到ρ=3cosθ即为所求
(2)由(1)知,点P的轨迹以(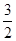 ,0)为圆心,半径为
,0)为圆心,半径为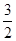 的圆,显然圆与x轴的交点(除原点)与直线x=4的最小距离为1,所以RP的最小值为1
的圆,显然圆与x轴的交点(除原点)与直线x=4的最小距离为1,所以RP的最小值为1
(1)设动点P的坐标为(ρ,θ),M的坐标为(ρ0,θ),则ρρ0=12,由ρ0cosθ=4,得到ρ=3cosθ即为所求
(2)由(1)知,点P的轨迹以(
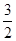 ,0)为圆心,半径为
,0)为圆心,半径为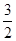 的圆,显然圆与x轴的交点(除原点)与直线x=4的最小距离为1,所以RP的最小值为1
的圆,显然圆与x轴的交点(除原点)与直线x=4的最小距离为1,所以RP的最小值为1
练习册系列答案
相关题目
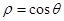 与
与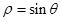 的两个圆的圆心距为_____________
的两个圆的圆心距为_____________ 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为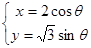 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程; 两点,求弦
两点,求弦 的长.
的长. (t为参数)所表示的图形分别为( )
(t为参数)所表示的图形分别为( )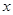 轴非负半轴重合.直线
轴非负半轴重合.直线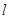 的参数方程为:
的参数方程为: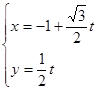 (
(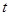 为参数),曲线
为参数),曲线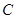 的极坐标方程为:
的极坐标方程为: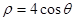 .
.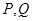 两点,求
两点,求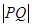 的值.2
的值.2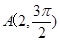 处并且过极点的圆的极坐标方程,并把它化为直角坐标方程。
处并且过极点的圆的极坐标方程,并把它化为直角坐标方程。 轴的正半轴重合.直线
轴的正半轴重合.直线 的参数方程为:
的参数方程为: (t为参数),曲线
(t为参数),曲线 的极坐标方程为:
的极坐标方程为: .
. 、
、 两点,求
两点,求 值.
值. :
: (
(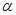 为参数,
为参数,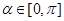 )上,点Q在曲线
)上,点Q在曲线 :
: 上
上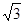 ),则点P的极坐标为( )
),则点P的极坐标为( )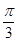 )
) )
)