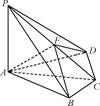
题目内容
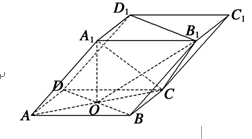
如图,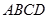 是边长为
是边长为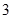 的正方形,
的正方形,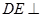 平面
平面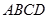 ,
,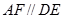 ,
,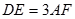 ,
,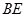 与平面
与平面 所成角为
所成角为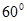 .
.
(1)求证: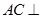 平面
平面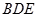 ;
;
(2)求二面角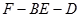 的余弦值;
的余弦值;
(3)设点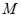 是线段
是线段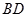 上一个动点,试确定点
上一个动点,试确定点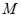 的位置,使得
的位置,使得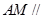 平面
平面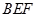 ,并证明你的结论.
,并证明你的结论.
(1) 参考解析;(2) 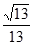 ; (3)
; (3) 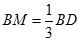
解析试题分析:(1)因为要证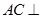 平面
平面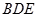 即直线与平面垂直的证明,通过证明这条直线垂直平面内的两条相交直线即可,依题意易得到.
即直线与平面垂直的证明,通过证明这条直线垂直平面内的两条相交直线即可,依题意易得到.
(2)因为要求二面角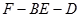 的余弦值,一般是通过建立空间坐标系,写出相应的点的坐标,由于AC所在的向量就是平面EDB的法向量,所以关键是通过待定系数法求出平面EFB的法向量.再通过两法向量的夹角得到两平面的二面角的大小,二面角是钝角还是锐角通过图形来确定.
的余弦值,一般是通过建立空间坐标系,写出相应的点的坐标,由于AC所在的向量就是平面EDB的法向量,所以关键是通过待定系数法求出平面EFB的法向量.再通过两法向量的夹角得到两平面的二面角的大小,二面角是钝角还是锐角通过图形来确定.
(3)因为点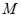 是线段
是线段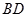 上一个动点,试确定点
上一个动点,试确定点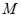 的位置,使得
的位置,使得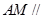 平面
平面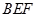 .通过对点M的假设写出向量AM.从而由该向量垂直平面的法向量,即可得到相应的点M的坐标.
.通过对点M的假设写出向量AM.从而由该向量垂直平面的法向量,即可得到相应的点M的坐标.
试题解析:(1)证明: 因为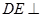 平面
平面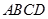 , 所以
, 所以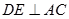 .
.
因为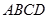 是正方形,所以
是正方形,所以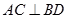 ,又
,又 相交
相交
从而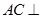 平面
平面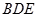 .
.
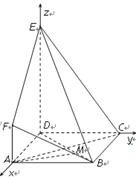
(2)解:因为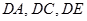 两两垂直,所以建立空间直角坐标系
两两垂直,所以建立空间直角坐标系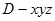 如图所示.因为
如图所示.因为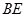 与平面
与平面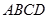 所成角为
所成角为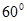 , 即
, 即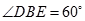 ,
,
所以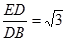 .由
.由 可知
可知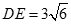 ,
,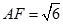 .
.
则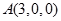 ,
, ,
,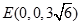 ,
,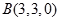 ,
,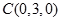 ,
,
所以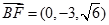 ,
,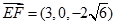 ,
,
设平面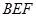 的法向量为
的法向量为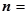
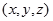 ,则
,则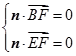 ,即
,即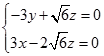 ,
,
令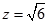 ,则
,则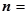
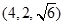 . 因为
. 因为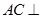 平面
平面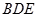 ,所以
,所以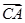 为平面
为平面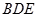 的法向量,
的法向量,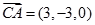 ,
,
所以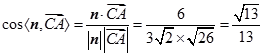 .
.
因为二面角为锐角,所以二面角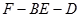 的余弦值为
的余弦值为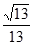 .
.
(3)解:点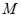 是线段
是线段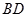 上一个动点,设
上一个动点,设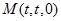 . 则
. 则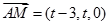 ,
,
因为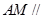 平面
平面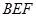 ,所以
,所以
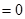 ,
,
即 ,解得
,解得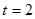 .
.
此时,点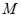 坐标为
坐标为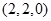 ,
,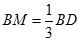 ,符合题意.
,符合题意.
考点:1.线面垂直的证明.2.二面角的问题.3.直线与平面平行.4.空间想象能力.

练习册系列答案
相关题目
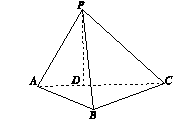
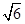 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD= .
.
 .
.
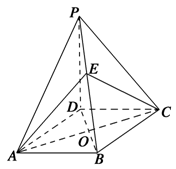
 的底面
的底面 是正方形,
是正方形, 底面
底面 是
是 上的任意一点.
上的任意一点.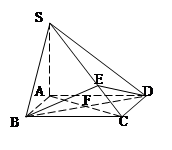
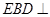 平面
平面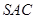 ;
;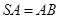 时,求二面角
时,求二面角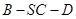 的大小.
的大小.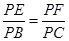 =λ.
=λ.
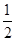 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;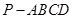 中,底面
中,底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面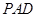
 底面
底面 .
.
 ;
; 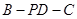 的余弦值.
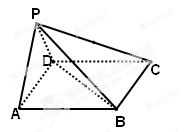
的余弦值.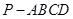 中,顶点
中,顶点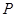 在底面
在底面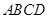 内的射影恰好落在
内的射影恰好落在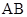 的中点
的中点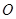 上,又
上,又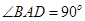 ,
,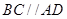 且
且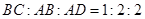
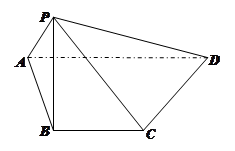
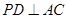 ;
;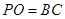 ,求直线
,求直线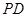 与
与 所成角的余弦值;
所成角的余弦值;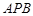 与平面
与平面 所成的角为
所成的角为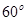 ,求
,求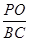 的值。
的值。 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.