题目内容
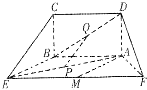
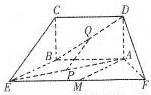 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
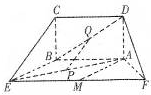
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=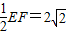 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.(I)求证:PQ∥平面BCE;
(II)求证:AM⊥平面ADF;
(III)求二面角A-DF-E的余弦值.
【答案】分析:(I)连结AC,证明PQ∥EC,利用直线与平面平行的判定定理证明PQ∥平面BCE;
(II)直接利用直线与平面垂直的判定定理证明AM⊥平面ADF;
(III)通过建立空间直角坐标系,求出两个平面的法向量,通过空间向量的数量积求出二面角A-DF-E的余弦值.
解答:解:(Ⅰ)连结AC,因为四边形ABCD是矩形,
Q为BD的中点,所以Q为AC的中点,
又在△AEC中,P为AE的中点,∴PQ∥EC,
∵EC?平面BCE中,PQ?平面BSE,
∴PQ∥平面BCE;
(Ⅱ)∵M为EF的中点,∴EM=AB=2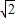 ,
,
又∵EF∥AB,∴四边形ABEM是平行四边形,
又AF=2,MF=2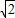 ,∴△MAF是直角三角形,∠MAF=90°,
,∴△MAF是直角三角形,∠MAF=90°,
∴MA⊥AF,
∵DA⊥面ABEF,MA?平面ABEF,∴MA⊥DA,
又∵DA∩AF=A,
∴AM⊥平面ADF;
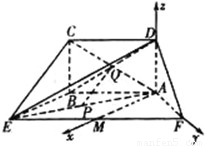
(Ⅲ)如图,以A坐标原点,建立空间直角坐标系,则A(0,0,0),D(0,0,1),M(2,0,0),F(0,2,0).
可得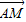 =(2,0,0),
=(2,0,0), ,
, ,
,
设平面DEF的法向量为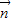 =(x,y,z),
=(x,y,z),
则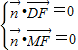 故
故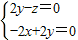
令x=1,则y=1,z=2故 .
.
∵AM⊥平面ADF,
所以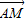 为平面ADF的一个法向量,
为平面ADF的一个法向量,
所以 ,
,
所以所求二面角A-DF-E的余弦值为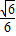 .
.
点评:本题考查直线与平面平行与垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力与计算能力.
(II)直接利用直线与平面垂直的判定定理证明AM⊥平面ADF;
(III)通过建立空间直角坐标系,求出两个平面的法向量,通过空间向量的数量积求出二面角A-DF-E的余弦值.
解答:解:(Ⅰ)连结AC,因为四边形ABCD是矩形,
Q为BD的中点,所以Q为AC的中点,
又在△AEC中,P为AE的中点,∴PQ∥EC,
∵EC?平面BCE中,PQ?平面BSE,
∴PQ∥平面BCE;
(Ⅱ)∵M为EF的中点,∴EM=AB=2
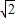 ,
,又∵EF∥AB,∴四边形ABEM是平行四边形,
又AF=2,MF=2
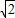 ,∴△MAF是直角三角形,∠MAF=90°,
,∴△MAF是直角三角形,∠MAF=90°,∴MA⊥AF,
∵DA⊥面ABEF,MA?平面ABEF,∴MA⊥DA,
又∵DA∩AF=A,
∴AM⊥平面ADF;

(Ⅲ)如图,以A坐标原点,建立空间直角坐标系,则A(0,0,0),D(0,0,1),M(2,0,0),F(0,2,0).
可得
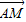 =(2,0,0),
=(2,0,0), ,
, ,
,设平面DEF的法向量为
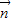 =(x,y,z),
=(x,y,z),则
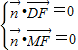 故
故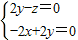
令x=1,则y=1,z=2故
 .
.∵AM⊥平面ADF,
所以
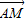 为平面ADF的一个法向量,
为平面ADF的一个法向量,所以
 ,
,所以所求二面角A-DF-E的余弦值为
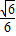 .
.点评:本题考查直线与平面平行与垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力与计算能力.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
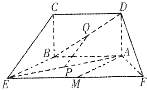 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,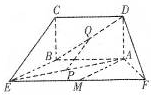 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB= 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,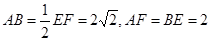 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.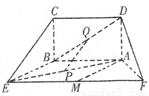
 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,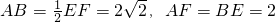 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.