题目内容
（13分）已知椭圆C：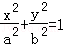
（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点
．
（I）求椭圆C的离心率：
（II）设过点A（0，2）的直线l与椭圆C交于M，N两点，点Q是线段MN上的点，且
，求点Q的轨迹方程．
【答案】
（I）
（II）点Q的轨迹方程为10（y﹣2）2﹣3x2=18，其中x∈（﹣
，），y∈（
，2﹣
）
【解析】（I）∵椭圆C：
（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点
．
∴c=1，2a=PF1+PF2=
=2
，即a=
∴椭圆的离心率e=
=
=…4分
（II）由（I）知，椭圆C的方程为
，设点Q的坐标为（x，y）
（1）当直线l与x轴垂直时，直线l与椭圆C交于（0，1）、（0，﹣1）两点，此时点Q的坐标为（0，2﹣
）
（2）当直线l与x轴不垂直时，可设其方程为y=kx+2，
因为M，N在直线l上，可设点M，N的坐标分别为（x1，kx1+2），（x2，kx2+2），则
，
，又|AQ|2=（1+k2）x2，
∴
，即
=
…①
将y=kx+2代入
中，得（2k2+1）x2+8kx+6=0…②
由△=（8k）2﹣24（2k2+1）＞0，得k2＞
由②知x1+x2=
，x1x2=
，代入①中化简得x2=
…③
因为点Q在直线y=kx+2上，所以k=
，代入③中并化简得10（y﹣2）2﹣3x2=18
由③及k2＞
可知0＜x＜，即x∈（﹣
，0）∪（0，）
由题意，Q（x，y）在椭圆C内，所以﹣1≤y≤1，
又由10（y﹣2）2﹣3x2=18得（y﹣2）2∈[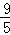
，
）且﹣1≤y≤1，则y∈（，2﹣）
所以，点Q的轨迹方程为10（y﹣2）2﹣3x2=18，其中x∈（﹣，），y∈（，2﹣）…13分
练习册系列答案
名校课堂系列答案
相关题目
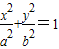（a＞b＞0）的左、右焦点分别为F1（-1，0）、F2（1，0），离心率为
．
（O为坐标原点），求△AOB的面积；
（a＞b＞0）的一个顶点为A（2,0），离心率为
，直线y=k（x-1）与椭圆C交于不同的两点M、N.
时，求k的值.
+
=1(a＞b＞0)，直线y=x+
与以原点为圆心，以椭圆C的短半轴长为半径的圆相切，F1，F2为其左、右焦点，P为椭圆C上任一点，△F1PF2的重心为G，内心为I，且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L：y=kx+m(k≠0)与椭圆C交于不同两点A，B且线段AB的垂直平分线过定点C(
，0)求实数k的取值范围。
（a>b>0）的离心率为
，过右焦点F且斜率为k（k>0）的直线与椭圆C相交于A、B两点，若
。则
（ ） 
（D）