题目内容
设x、y满足条件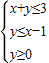
，则z=（x+1）2+y2的最小值（ ）A．4
B．2
C．16
D．10
【答案】分析：画出满足条件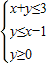
的平面区域，并分析z=（x+1）2+y2的几何意义，数形结合即可得到答案．
解答：解：满足条件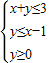
的平面区域如下图所示：
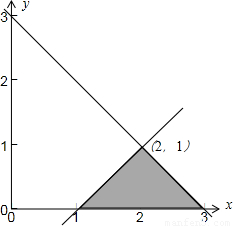
由z=（x+1）2+y2的表示（-1，0）点到可行域内点的距离的平方
故当x=1，y=0时，Z有最小值4
故选A
点评：本题考查的知识点是简单线性规划，其中根据约束条件画出可行域，并分析目标函数的几何意义是解答本题的关键．
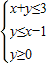的平面区域，并分析z=（x+1）2+y2的几何意义，数形结合即可得到答案．解答：解：满足条件
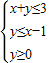的平面区域如下图所示：由z=（x+1）2+y2的表示（-1，0）点到可行域内点的距离的平方
故当x=1，y=0时，Z有最小值4
故选A
点评：本题考查的知识点是简单线性规划，其中根据约束条件画出可行域，并分析目标函数的几何意义是解答本题的关键．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
，则目标函数z=x+2y的最大值为（ ）
，则z=（x+1）2+y2的最小值 ．
，则
的最大值为（ ）
，则
的最小值 ．
，则z=（x+1）2+y2的最小值 ．